Menu Close

calculate-0-logx-x-6-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 143545 by mathmax by abdo last updated on 15/Jun/21
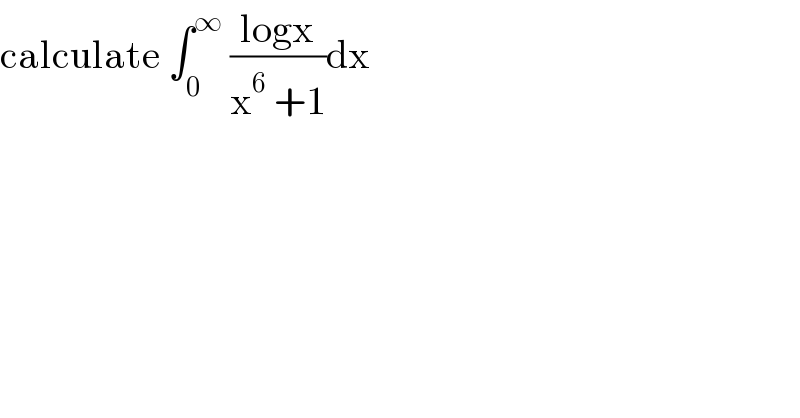
calculate ∫_0 ^∞ ((logx)/(x^6 +1))dx
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logx}}{\mathrm{x}^{\mathrm{6}} \:+\mathrm{1}}\mathrm{dx} \\ $$
Answered by Pagnol last updated on 15/Jun/21
I=∫_0 ^∞ ((logx)/(x^6 +1))dx , u=x^6 ⇒x=u^(1/6) ⇒dx=(1/6)u^(−(5/6)) du =(1/(36))∫_0 ^∞ ((u^(−(5/6)) logu)/(u+1))du I(α)=∫_0 ^∞ (u^α /(u+1))du=β(α+1, −α)=((Γ(α+1)Γ(−α))/(Γ(1))) I′(α)=∫_0 ^∞ ((u^α lnu)/(u+1))du=−Γ(α+1)Γ′(−α)+Γ′(α+1)Γ(−α) I′(−(5/6))=−Γ((1/6))Γ′((5/6))+Γ′((1/6))Γ((5/6)) =Γ((1/6))Γ((5/6))[ψ((1/6))−ψ((5/6))] =(π/(sin((π/6))))[−πcot((5/6)π)]=2π(π(√3))=2(√3)π^2 I=(1/(36))I′(−(5/6))=((√3)/(18))π^2
$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{logx}}{\mathrm{x}^{\mathrm{6}} +\mathrm{1}}\mathrm{dx}\:,\:\mathrm{u}=\mathrm{x}^{\mathrm{6}} \Rightarrow\mathrm{x}=\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{6}}} \Rightarrow\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{u}^{−\frac{\mathrm{5}}{\mathrm{6}}} \mathrm{du} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{36}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{−\frac{\mathrm{5}}{\mathrm{6}}} \mathrm{logu}}{\mathrm{u}+\mathrm{1}}\mathrm{du} \\ $$$$\mathrm{I}\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{\alpha} }{\mathrm{u}+\mathrm{1}}\mathrm{du}=\beta\left(\alpha+\mathrm{1},\:−\alpha\right)=\frac{\Gamma\left(\alpha+\mathrm{1}\right)\Gamma\left(−\alpha\right)}{\Gamma\left(\mathrm{1}\right)} \\ $$$$\mathrm{I}'\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{\alpha} \mathrm{lnu}}{\mathrm{u}+\mathrm{1}}\mathrm{du}=−\Gamma\left(\alpha+\mathrm{1}\right)\Gamma'\left(−\alpha\right)+\Gamma'\left(\alpha+\mathrm{1}\right)\Gamma\left(−\alpha\right) \\ $$$$\mathrm{I}'\left(−\frac{\mathrm{5}}{\mathrm{6}}\right)=−\Gamma\left(\frac{\mathrm{1}}{\mathrm{6}}\right)\Gamma'\left(\frac{\mathrm{5}}{\mathrm{6}}\right)+\Gamma'\left(\frac{\mathrm{1}}{\mathrm{6}}\right)\Gamma\left(\frac{\mathrm{5}}{\mathrm{6}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\Gamma\left(\frac{\mathrm{1}}{\mathrm{6}}\right)\Gamma\left(\frac{\mathrm{5}}{\mathrm{6}}\right)\left[\psi\left(\frac{\mathrm{1}}{\mathrm{6}}\right)−\psi\left(\frac{\mathrm{5}}{\mathrm{6}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{6}}\right)}\left[−\pi\mathrm{cot}\left(\frac{\mathrm{5}}{\mathrm{6}}\pi\right)\right]=\mathrm{2}\pi\left(\pi\sqrt{\mathrm{3}}\right)=\mathrm{2}\sqrt{\mathrm{3}}\pi^{\mathrm{2}} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{36}}\mathrm{I}'\left(−\frac{\mathrm{5}}{\mathrm{6}}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\pi^{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 15/Jun/21
Φ=∫_0 ^∞ ((logx)/(x^6 +1))dx changement x^6 =t give Φ=(1/6)∫_0 ^∞ ((log(t^(1/6) ))/(1+t))t^((1/6)−1) dt =(1/(36))∫_0 ^∞ ((t^((1/6)−1) logt)/(1+t))dt let f(a)=∫_0 ^∞ (t^(a−1) /(1+t))dt ⇒f^′ (a)=∫_0 ^∞ ((t^(a−1) logt)/(1+t))dt ⇒f^′ ((1/6))=36Φ ⇒ Φ=(1/(36))f^′ ((1/6)) we know f(a)=(π/(sin(πa))) ⇒f^′ (a)=−((π^2 cos(πa))/(sin^2 (πa))) ⇒ f^′ ((1/6))=−((π^2 ×((√3)/2))/(((1/2))^2 )) =−4π^2 .((√3)/2)=−2π^2 (√3) ⇒ Φ=(1/(36))(−2π^2 (√3)) =−(π^2 /(18))(√3)
$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logx}}{\mathrm{x}^{\mathrm{6}} \:+\mathrm{1}}\mathrm{dx}\:\mathrm{changement}\:\mathrm{x}^{\mathrm{6}} \:=\mathrm{t}\:\mathrm{give} \\ $$$$\Phi=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{log}\left(\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{6}}} \right)}{\mathrm{1}+\mathrm{t}}\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} \mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{36}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} \:\mathrm{logt}}{\mathrm{1}+\mathrm{t}}\mathrm{dt} \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{a}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\mathrm{a}−\mathrm{1}} \mathrm{logt}}{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:\Rightarrow\mathrm{f}^{'} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)=\mathrm{36}\Phi\:\Rightarrow \\ $$$$\Phi=\frac{\mathrm{1}}{\mathrm{36}}\mathrm{f}^{'} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)\:\:\mathrm{we}\:\mathrm{know}\:\mathrm{f}\left(\mathrm{a}\right)=\frac{\pi}{\mathrm{sin}\left(\pi\mathrm{a}\right)}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=−\frac{\pi^{\mathrm{2}} \mathrm{cos}\left(\pi\mathrm{a}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\pi\mathrm{a}\right)}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)=−\frac{\pi^{\mathrm{2}} ×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:=−\mathrm{4}\pi^{\mathrm{2}} .\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=−\mathrm{2}\pi^{\mathrm{2}} \sqrt{\mathrm{3}}\:\Rightarrow \\ $$$$\Phi=\frac{\mathrm{1}}{\mathrm{36}}\left(−\mathrm{2}\pi^{\mathrm{2}} \:\sqrt{\mathrm{3}}\right)\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{18}}\sqrt{\mathrm{3}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *