Menu Close

calculate-0-pi-2-cos-2-x-cosx-sinx-dx-

Tinku Tara
Pin




Question Number 65691 by mathmax by abdo last updated on 02/Aug/19
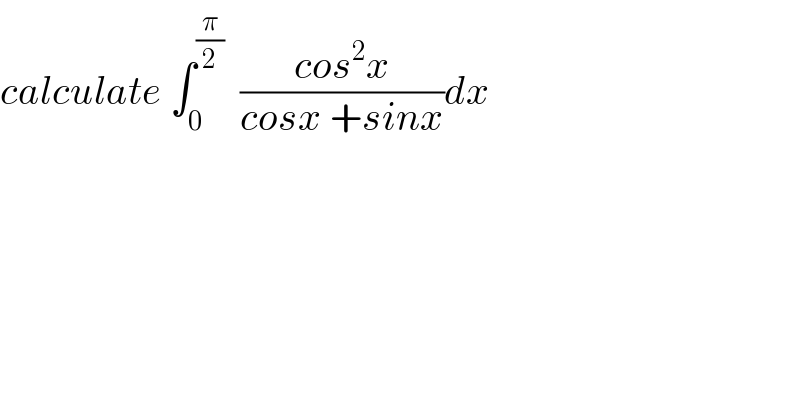
calculate ∫_0 ^(π/2) ((cos^2 x)/(cosx +sinx))dx
$${calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{cos}^{\mathrm{2}} {x}}{{cosx}\:+{sinx}}{dx} \\ $$
Commented by mathmax by abdo last updated on 02/Aug/19
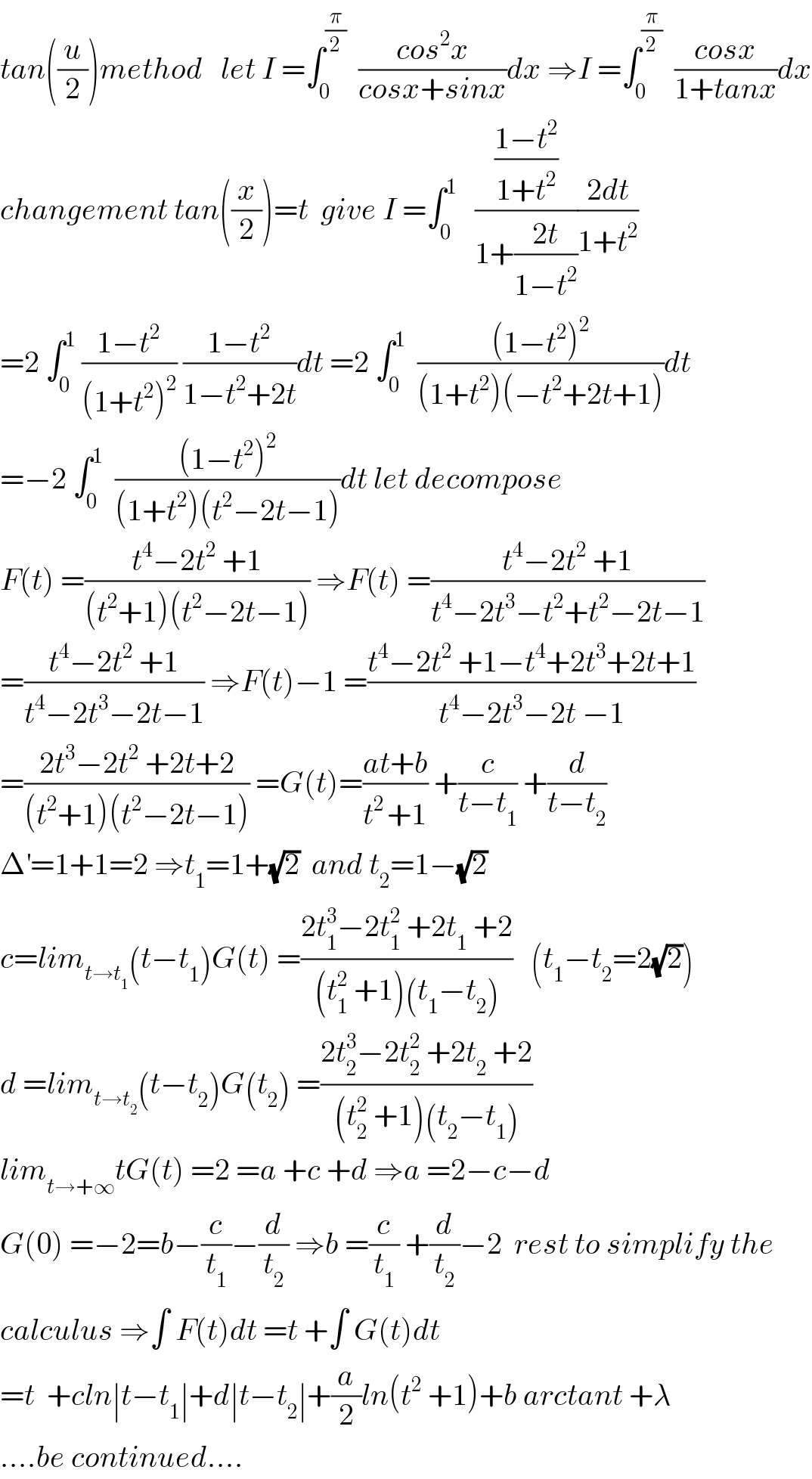
tan((u/2))method let I =∫_0 ^(π/2) ((cos^2 x)/(cosx+sinx))dx ⇒I =∫_0 ^(π/2) ((cosx)/(1+tanx))dx changement tan((x/2))=t give I =∫_0 ^1 (((1−t^2 )/(1+t^2 ))/(1+((2t)/(1−t^2 ))))((2dt)/(1+t^2 )) =2 ∫_0 ^1 ((1−t^2 )/((1+t^2 )^2 )) ((1−t^2 )/(1−t^2 +2t))dt =2 ∫_0 ^1 (((1−t^2 )^2 )/((1+t^2 )(−t^2 +2t+1)))dt =−2 ∫_0 ^1 (((1−t^2 )^2 )/((1+t^2 )(t^2 −2t−1)))dt let decompose F(t) =((t^4 −2t^2 +1)/((t^2 +1)(t^2 −2t−1))) ⇒F(t) =((t^4 −2t^2 +1)/(t^4 −2t^3 −t^2 +t^2 −2t−1)) =((t^4 −2t^2 +1)/(t^4 −2t^3 −2t−1)) ⇒F(t)−1 =((t^4 −2t^2 +1−t^4 +2t^3 +2t+1)/(t^4 −2t^3 −2t −1)) =((2t^3 −2t^2 +2t+2)/((t^2 +1)(t^2 −2t−1))) =G(t)=((at+b)/(t^(2 ) +1)) +(c/(t−t_1 )) +(d/(t−t_2 )) Δ^′ =1+1=2 ⇒t_1 =1+(√2) and t_2 =1−(√2) c=lim_(t→t_1 ) (t−t_1 )G(t) =((2t_1 ^3 −2t_1 ^2 +2t_1 +2)/((t_1 ^2 +1)(t_1 −t_2 ))) (t_1 −t_2 =2(√2)) d =lim_(t→t_2 ) (t−t_2 )G(t_2 ) =((2t_2 ^3 −2t_2 ^2 +2t_2 +2)/((t_2 ^2 +1)(t_2 −t_1 ))) lim_(t→+∞) tG(t) =2 =a +c +d ⇒a =2−c−d G(0) =−2=b−(c/t_1 )−(d/t_2 ) ⇒b =(c/t_1 ) +(d/t_2 )−2 rest to simplify the calculus ⇒∫ F(t)dt =t +∫ G(t)dt =t +cln∣t−t_1 ∣+d∣t−t_2 ∣+(a/2)ln(t^2 +1)+b arctant +λ ....be continued....
$${tan}\left(\frac{{u}}{\mathrm{2}}\right){method}\:\:\:{let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{cos}^{\mathrm{2}} {x}}{{cosx}+{sinx}}{dx}\:\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{cosx}}{\mathrm{1}+{tanx}}{dx} \\ $$$${changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:\:{give}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }}\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}−{t}^{\mathrm{2}} +\mathrm{2}{t}}{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(−{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)}{dt} \\ $$$$=−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)}{dt}\:{let}\:{decompose}\: \\ $$$${F}\left({t}\right)\:=\frac{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)}\:\Rightarrow{F}\left({t}\right)\:=\frac{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} −{t}^{\mathrm{2}} +{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}} \\ $$$$=\frac{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} −\mathrm{2}{t}−\mathrm{1}}\:\Rightarrow{F}\left({t}\right)−\mathrm{1}\:=\frac{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}−{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}{t}+\mathrm{1}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} −\mathrm{2}{t}\:−\mathrm{1}} \\ $$$$=\frac{\mathrm{2}{t}^{\mathrm{3}} −\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{2}{t}+\mathrm{2}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)}\:={G}\left({t}\right)=\frac{{at}+{b}}{{t}^{\mathrm{2}\:} +\mathrm{1}}\:+\frac{{c}}{{t}−{t}_{\mathrm{1}} }\:+\frac{{d}}{{t}−{t}_{\mathrm{2}} } \\ $$$$\Delta^{'} =\mathrm{1}+\mathrm{1}=\mathrm{2}\:\Rightarrow{t}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{2}}\:\:{and}\:{t}_{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{2}} \\ $$$${c}={lim}_{{t}\rightarrow{t}_{\mathrm{1}} } \left({t}−{t}_{\mathrm{1}} \right){G}\left({t}\right)\:=\frac{\mathrm{2}{t}_{\mathrm{1}} ^{\mathrm{3}} −\mathrm{2}{t}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{2}{t}_{\mathrm{1}} \:+\mathrm{2}}{\left({t}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}_{\mathrm{1}} −{t}_{\mathrm{2}} \right)}\:\:\:\left({t}_{\mathrm{1}} −{t}_{\mathrm{2}} =\mathrm{2}\sqrt{\mathrm{2}}\right) \\ $$$${d}\:={lim}_{{t}\rightarrow{t}_{\mathrm{2}} } \left({t}−{t}_{\mathrm{2}} \right){G}\left({t}_{\mathrm{2}} \right)\:=\frac{\mathrm{2}{t}_{\mathrm{2}} ^{\mathrm{3}} −\mathrm{2}{t}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{2}{t}_{\mathrm{2}} \:+\mathrm{2}}{\left({t}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)} \\ $$$${lim}_{{t}\rightarrow+\infty} {tG}\left({t}\right)\:=\mathrm{2}\:={a}\:+{c}\:+{d}\:\Rightarrow{a}\:=\mathrm{2}−{c}−{d} \\ $$$${G}\left(\mathrm{0}\right)\:=−\mathrm{2}={b}−\frac{{c}}{{t}_{\mathrm{1}} }−\frac{{d}}{{t}_{\mathrm{2}} }\:\Rightarrow{b}\:=\frac{{c}}{{t}_{\mathrm{1}} }\:+\frac{{d}}{{t}_{\mathrm{2}} }−\mathrm{2}\:\:{rest}\:{to}\:{simplify}\:{the} \\ $$$${calculus}\:\Rightarrow\int\:{F}\left({t}\right){dt}\:={t}\:+\int\:{G}\left({t}\right){dt} \\ $$$$={t}\:\:+{cln}\mid{t}−{t}_{\mathrm{1}} \mid+{d}\mid{t}−{t}_{\mathrm{2}} \mid+\frac{{a}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)+{b}\:{arctant}\:+\lambda \\ $$$$….{be}\:{continued}…. \\ $$
Answered by Tanmay chaudhury last updated on 02/Aug/19
I=∫_0 ^(π/2) ((cos^2 x)/(cosx+sinx))dx I=∫_0 ^(π/2) ((cos^2 ((π/2)−x))/(cos((π/2)−x)+sin((π/2)−x)))dx =∫_0 ^(π/2) ((sin^2 x)/(sinx+cosx))dx 2I=∫_0 ^(π/2) (dx/(sinx+cosx)) 2I=∫_0 ^(π/2) (dx/( (√2) ((1/( (√2)))sinx+(1/( (√2)))cosx))) I=(1/(2(√2)))∫_0 ^(π/2) (dx/(sin((π/4)+x))) I=(1/(2(√2)))∫_0 ^(π/4) cosec((π/4)+x)dx I=(1/(2(√2)))∣lntan((((π/4)+x)/2))∣_0 ^(π/4) =(1/(2(√2)))[lntan((π/4))−lntan((π/8))] =((−1)/(2(√2)))lntan((π/8))
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{2}} {x}}{{cosx}+{sinx}}{dx} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)}{{cos}\left(\frac{\pi}{\mathrm{2}}−{x}\right)+{sin}\left(\frac{\pi}{\mathrm{2}}−{x}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2}} {x}}{{sinx}+{cosx}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{{sinx}+{cosx}} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\:\sqrt{\mathrm{2}}\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{sinx}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{cosx}\right)} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{{sin}\left(\frac{\pi}{\mathrm{4}}+{x}\right)} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {cosec}\left(\frac{\pi}{\mathrm{4}}+{x}\right){dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mid{lntan}\left(\frac{\frac{\pi}{\mathrm{4}}+{x}}{\mathrm{2}}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left[{lntan}\left(\frac{\pi}{\mathrm{4}}\right)−{lntan}\left(\frac{\pi}{\mathrm{8}}\right)\right] \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{lntan}\left(\frac{\pi}{\mathrm{8}}\right) \\ $$
Commented by mathmax by abdo last updated on 02/Aug/19
thank you sir tanmay
$${thank}\:{you}\:{sir}\:{tanmay} \\ $$
Commented by Tanmay chaudhury last updated on 02/Aug/19
most eelcome sir...
$${most}\:{eelcome}\:{sir}… \\ $$
Commented by peter frank last updated on 02/Aug/19
thank you
$${thank}\:{you} \\ $$

Pin