Menu Close

calculate-0-pi-4-ln-cosx-dx-and-0-pi-4-ln-sinx-dx-

Tinku Tara 0 Comments
Pin




Question Number 70262 by mathmax by abdo last updated on 02/Oct/19
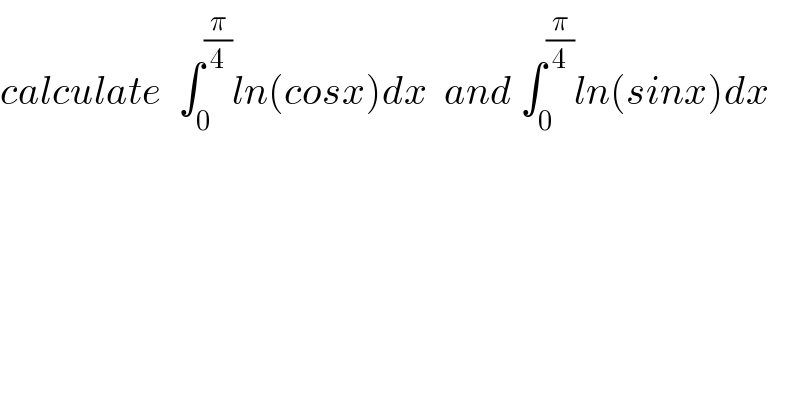
calculate ∫_0 ^(π/4) ln(cosx)dx and ∫_0 ^(π/4) ln(sinx)dx
$${calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cosx}\right){dx}\:\:{and}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sinx}\right){dx} \\ $$
Commented by mathmax by abdo last updated on 06/Oct/19
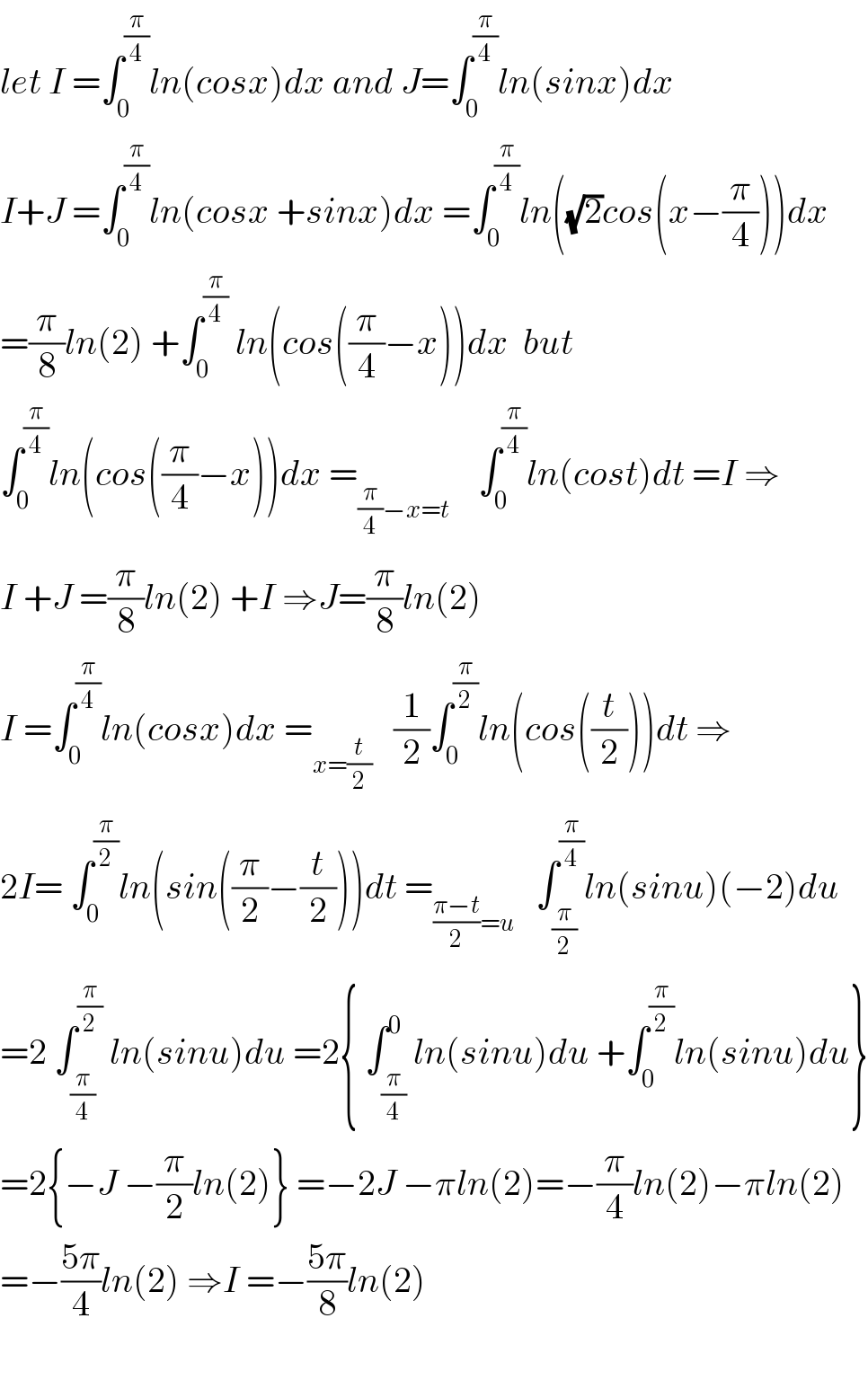
let I =∫_0 ^(π/4) ln(cosx)dx and J=∫_0 ^(π/4) ln(sinx)dx I+J =∫_0 ^(π/4) ln(cosx +sinx)dx =∫_0 ^(π/4) ln((√2)cos(x−(π/4)))dx =(π/8)ln(2) +∫_0 ^(π/4) ln(cos((π/4)−x))dx but ∫_0 ^(π/4) ln(cos((π/4)−x))dx =_((π/4)−x=t) ∫_0 ^(π/4) ln(cost)dt =I ⇒ I +J =(π/8)ln(2) +I ⇒J=(π/8)ln(2) I =∫_0 ^(π/4) ln(cosx)dx =_(x=(t/2)) (1/2)∫_0 ^(π/2) ln(cos((t/2)))dt ⇒ 2I= ∫_0 ^(π/2) ln(sin((π/2)−(t/2)))dt =_(((π−t)/2)=u) ∫_(π/2) ^(π/4) ln(sinu)(−2)du =2 ∫_(π/4) ^(π/2) ln(sinu)du =2{ ∫_(π/4) ^0 ln(sinu)du +∫_0 ^(π/2) ln(sinu)du} =2{−J −(π/2)ln(2)} =−2J −πln(2)=−(π/4)ln(2)−πln(2) =−((5π)/4)ln(2) ⇒I =−((5π)/8)ln(2)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cosx}\right){dx}\:{and}\:{J}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sinx}\right){dx} \\ $$$${I}+{J}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cosx}\:+{sinx}\right){dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\sqrt{\mathrm{2}}{cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)\right){dx} \\ $$$$=\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right)\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{ln}\left({cos}\left(\frac{\pi}{\mathrm{4}}−{x}\right)\right){dx}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left(\frac{\pi}{\mathrm{4}}−{x}\right)\right){dx}\:=_{\frac{\pi}{\mathrm{4}}−{x}={t}} \:\:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cost}\right){dt}\:={I}\:\Rightarrow \\ $$$${I}\:+{J}\:=\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right)\:+{I}\:\Rightarrow{J}=\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right) \\ $$$${I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cosx}\right){dx}\:=_{{x}=\frac{{t}}{\mathrm{2}}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cos}\left(\frac{{t}}{\mathrm{2}}\right)\right){dt}\:\Rightarrow \\ $$$$\mathrm{2}{I}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left(\frac{\pi}{\mathrm{2}}−\frac{{t}}{\mathrm{2}}\right)\right){dt}\:=_{\frac{\pi−{t}}{\mathrm{2}}={u}} \:\:\:\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sinu}\right)\left(−\mathrm{2}\right){du} \\ $$$$=\mathrm{2}\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left({sinu}\right){du}\:=\mathrm{2}\left\{\:\int_{\frac{\pi}{\mathrm{4}}} ^{\mathrm{0}} {ln}\left({sinu}\right){du}\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sinu}\right){du}\right\} \\ $$$$=\mathrm{2}\left\{−{J}\:−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\right\}\:=−\mathrm{2}{J}\:−\pi{ln}\left(\mathrm{2}\right)=−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−\pi{ln}\left(\mathrm{2}\right) \\ $$$$=−\frac{\mathrm{5}\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)\:\Rightarrow{I}\:=−\frac{\mathrm{5}\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right) \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *