Menu Close

calculate-0-sin-3x-2-x-2-dx-

Tinku Tara
Pin




Question Number 65922 by mathmax by abdo last updated on 05/Aug/19
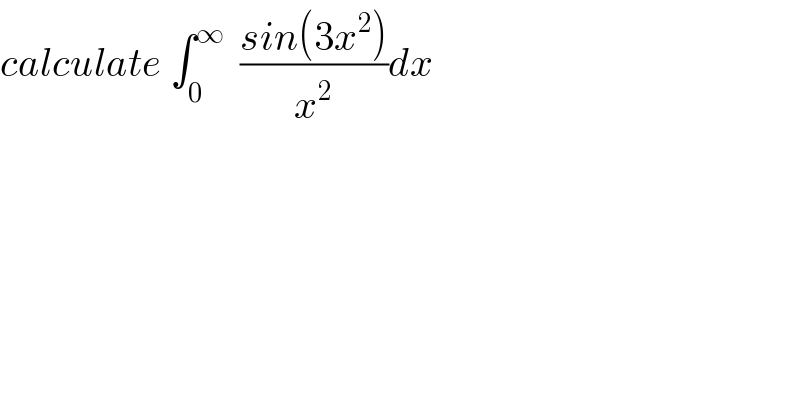
calculate ∫_0 ^∞ ((sin(3x^2 ))/x^2 )dx
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left(\mathrm{3}{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }{dx}\: \\ $$
Commented by mathmax by abdo last updated on 08/Aug/19
let A =∫_0 ^∞ ((sin(3x^2 ))/x^2 )dx ⇒A =_((√3)x =t) 3∫_0 ^∞ ((sin(t^2 ))/t^2 )(dt/( (√3))) =(1/( (√3)))∫_0 ^∞ ((sin(t^2 ))/t^2 )dt let ϕ(x) =∫_0 ^∞ ((sin(t^2 )e^(−xt^2 ) )/t^2 )dt with x≥0 ϕ^′ (x) =−∫_0 ^∞ e^(−xt^2 ) sin(t^2 )dt =−Im(∫_0 ^∞ e^(−xt^2 +it^2 ) dt) and ∫_0 ^∞ e^((−x+i)t^2 ) dt =_((√(−x+i))t =u) ∫_0 ^∞ e^(−u^2 ) (du/( (√(−x+i)))) =((√π)/(2(√(−x+i)))) ⇒ϕ(x) =((√π)/2)∫ (dx/( (√(−x+i)))) +c −x+i =(√(1+x^2 )) e^(iarctan(−(1/x))) =(√(1+x^2 ))e^(−i arctan((1/x))) =(√(1+x^2 )) e^(−i((π/2)−arctanx)) =−i(√(1+x^2 ))e^(iatctanx) ⇒ (√(−x+i)) =(√(−i))(1+x^2 )^(1/4) e^((i/2)arctan(x)) =e^(−((iπ)/4)) (1+x^2 )^(1/4) e^((i/2)arctanx) ⇒ ϕ(x) =((√π)/2) e^((iπ)/4) ∫ (1+x^2 )^(−(1/4)) e^(−(i/2)arctanx) dx +c ....be continued....
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left(\mathrm{3}{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }{dx}\:\Rightarrow{A}\:=_{\sqrt{\mathrm{3}}{x}\:={t}} \:\:\:\mathrm{3}\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}\left({t}^{\mathrm{2}} \right)}{{t}^{\mathrm{2}} }\frac{{dt}}{\:\sqrt{\mathrm{3}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left({t}^{\mathrm{2}} \right)}{{t}^{\mathrm{2}} }{dt}\:\:{let}\:\varphi\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left({t}^{\mathrm{2}} \right){e}^{−{xt}^{\mathrm{2}} } }{{t}^{\mathrm{2}} }{dt}\:\:{with}\:{x}\geqslant\mathrm{0} \\ $$$$\varphi^{'} \left({x}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{xt}^{\mathrm{2}} } {sin}\left({t}^{\mathrm{2}} \right){dt}\:=−{Im}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}^{\mathrm{2}} +{it}^{\mathrm{2}} } {dt}\right)\:{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−{x}+{i}\right){t}^{\mathrm{2}} } {dt}\:=_{\sqrt{−{x}+{i}}{t}\:={u}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}^{\mathrm{2}} } \frac{{du}}{\:\sqrt{−{x}+{i}}} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{−{x}+{i}}}\:\Rightarrow\varphi\left({x}\right)\:=\frac{\sqrt{\pi}}{\mathrm{2}}\int\:\frac{{dx}}{\:\sqrt{−{x}+{i}}}\:+{c} \\ $$$$−{x}+{i}\:=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:{e}^{{iarctan}\left(−\frac{\mathrm{1}}{{x}}\right)} \:=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{e}^{−{i}\:{arctan}\left(\frac{\mathrm{1}}{{x}}\right)} \\ $$$$=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:{e}^{−{i}\left(\frac{\pi}{\mathrm{2}}−{arctanx}\right)} \:=−{i}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{e}^{{iatctanx}} \:\Rightarrow \\ $$$$\sqrt{−{x}+{i}}\:=\sqrt{−{i}}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left({x}\right)} \:={e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:{e}^{\frac{{i}}{\mathrm{2}}{arctanx}} \:\Rightarrow \\ $$$$\varphi\left({x}\right)\:=\frac{\sqrt{\pi}}{\mathrm{2}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\:\int\:\:\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{4}}} {e}^{−\frac{{i}}{\mathrm{2}}{arctanx}} {dx}\:+{c} \\ $$$$….{be}\:{continued}…. \\ $$

Pin