Menu Close

calculate-0-x-2-logx-x-6-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 142347 by mathmax by abdo last updated on 30/May/21
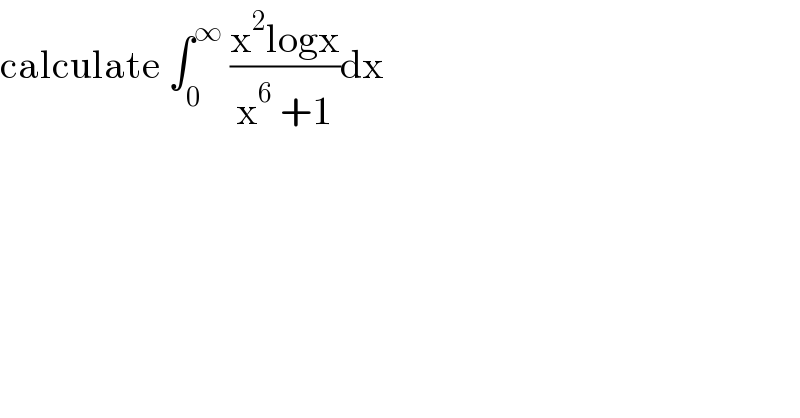
calculate ∫_0 ^∞ ((x^2 logx)/(x^6 +1))dx
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{logx}}{\mathrm{x}^{\mathrm{6}} \:+\mathrm{1}}\mathrm{dx} \\ $$
Commented by mathmax by abdo last updated on 31/May/21
Φ=∫_0 ^∞ ((x^2 logx)/(1+x^6 ))dx changement x=t^(1/6) give Φ=(1/6)∫_0 ^∞ ((t^(1/3) logt)/(1+t))(1/6)t^((1/6)−1) dt =(1/(36))∫_0 ^∞ (t^((1/3)+(1/6)−1) /(1+t))logt dt =(1/(36))∫_0 ^∞ (t^(−(1/2)) /(1+t))logt dt let f(a)=∫_0 ^∞ (t^(a−1) /(1+t)) dt we know f(a)=(π/(sin(πa))) (0<a<1) and f^′ (a) =∫_0 ^∞ (∂/∂a)( (e^((a−1)logt) /(1+t)))dt =∫_0 ^∞ (t^(a−1) /(1+t))logt dt but f^′ (a)=−π^2 ((cos(πa))/(sin^2 (πa))) ⇒Φ=(1/(36))∫_0 ^∞ (t^((1/2)−1) /(1+t))logt dt =(1/(36))f^′ ((1/2))=(1/(36))(−π^2 ).((cos((π/2)))/(sin^2 ((π/2)))) =0
$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{logx}}{\mathrm{1}+\mathrm{x}^{\mathrm{6}} }\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{6}}} \:\mathrm{give} \\ $$$$\Phi=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}} \mathrm{logt}}{\mathrm{1}+\mathrm{t}}\frac{\mathrm{1}}{\mathrm{6}}\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{36}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{logt}\:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{36}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}+\mathrm{t}}\mathrm{logt}\:\mathrm{dt} \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{a}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\:\mathrm{dt}\:\:\mathrm{we}\:\mathrm{know}\:\mathrm{f}\left(\mathrm{a}\right)=\frac{\pi}{\mathrm{sin}\left(\pi\mathrm{a}\right)}\:\:\left(\mathrm{0}<\mathrm{a}<\mathrm{1}\right) \\ $$$$\mathrm{and}\:\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\partial}{\partial\mathrm{a}}\left(\:\frac{\mathrm{e}^{\left(\mathrm{a}−\mathrm{1}\right)\mathrm{logt}} }{\mathrm{1}+\mathrm{t}}\right)\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{a}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{logt}\:\mathrm{dt} \\ $$$$\mathrm{but}\:\mathrm{f}^{'} \left(\mathrm{a}\right)=−\pi^{\mathrm{2}} \:\frac{\mathrm{cos}\left(\pi\mathrm{a}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\pi\mathrm{a}\right)} \\ $$$$\Rightarrow\Phi=\frac{\mathrm{1}}{\mathrm{36}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{logt}\:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{36}}\mathrm{f}^{'} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{36}}\left(−\pi^{\mathrm{2}} \right).\frac{\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}\right)} \\ $$$$=\mathrm{0} \\ $$
Answered by Dwaipayan Shikari last updated on 31/May/21
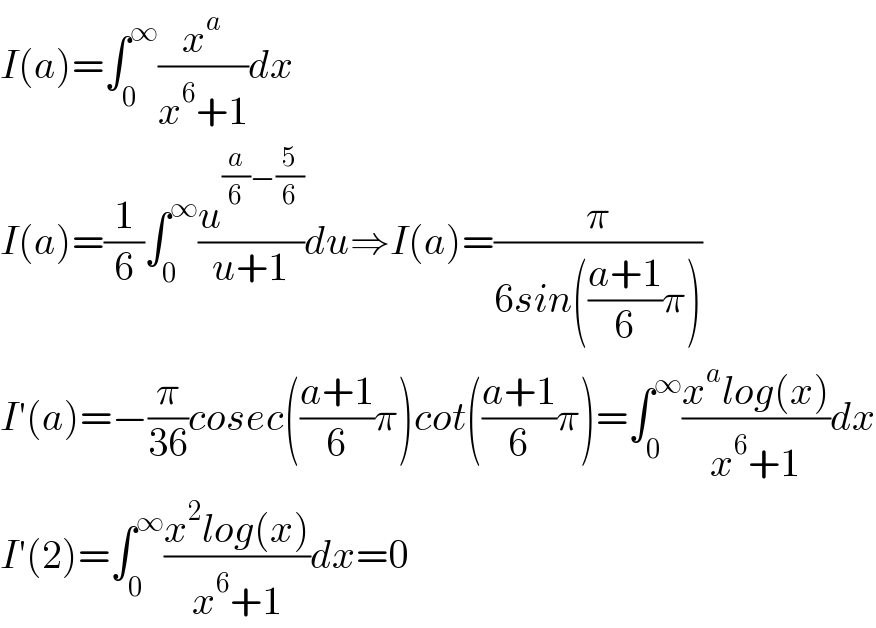
I(a)=∫_0 ^∞ (x^a /(x^6 +1))dx I(a)=(1/6)∫_0 ^∞ (u^((a/6)−(5/6)) /(u+1))du⇒I(a)=(π/(6sin(((a+1)/6)π))) I′(a)=−(π/(36))cosec(((a+1)/6)π)cot(((a+1)/6)π)=∫_0 ^∞ ((x^a log(x))/(x^6 +1))dx I′(2)=∫_0 ^∞ ((x^2 log(x))/(x^6 +1))dx=0
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}} }{{x}^{\mathrm{6}} +\mathrm{1}}{dx} \\ $$$${I}\left({a}\right)=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\frac{{a}}{\mathrm{6}}−\frac{\mathrm{5}}{\mathrm{6}}} }{{u}+\mathrm{1}}{du}\Rightarrow{I}\left({a}\right)=\frac{\pi}{\mathrm{6}{sin}\left(\frac{{a}+\mathrm{1}}{\mathrm{6}}\pi\right)} \\ $$$${I}'\left({a}\right)=−\frac{\pi}{\mathrm{36}}{cosec}\left(\frac{{a}+\mathrm{1}}{\mathrm{6}}\pi\right){cot}\left(\frac{{a}+\mathrm{1}}{\mathrm{6}}\pi\right)=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}} {log}\left({x}\right)}{{x}^{\mathrm{6}} +\mathrm{1}}{dx} \\ $$$${I}'\left(\mathrm{2}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} {log}\left({x}\right)}{{x}^{\mathrm{6}} +\mathrm{1}}{dx}=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *