Question Number 135368 by Bird last updated on 12/Mar/21
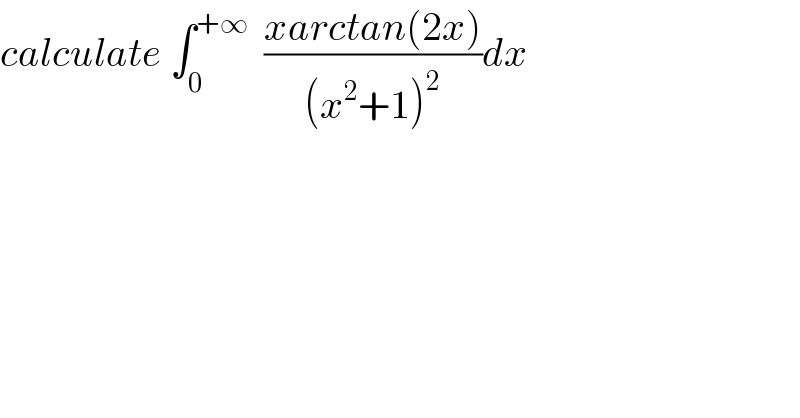
$${calculate}\:\int_{\mathrm{0}} ^{+\infty} \:\:\frac{{xarctan}\left(\mathrm{2}{x}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 12/Mar/21
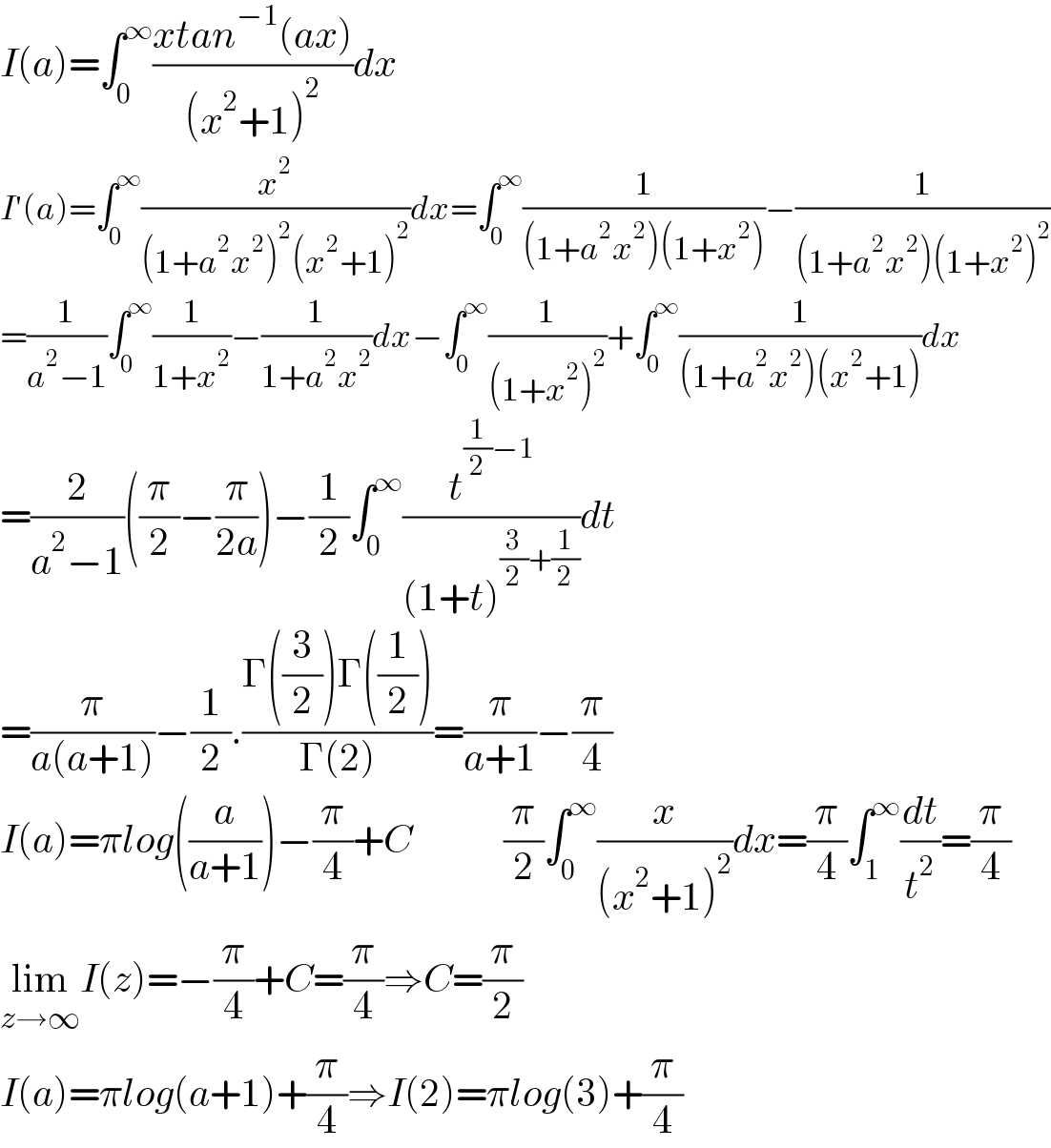
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{xtan}^{−\mathrm{1}} \left({ax}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$${I}'\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}−\frac{\mathrm{1}}{\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} }{dx}−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }+\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$$$=\frac{\mathrm{2}}{{a}^{\mathrm{2}} −\mathrm{1}}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{2}{a}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} }{\left(\mathrm{1}+{t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}} }{dt} \\ $$$$=\frac{\pi}{{a}\left({a}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}\right)}=\frac{\pi}{{a}+\mathrm{1}}−\frac{\pi}{\mathrm{4}} \\ $$$${I}\left({a}\right)=\pi{log}\left(\frac{{a}}{{a}+\mathrm{1}}\right)−\frac{\pi}{\mathrm{4}}+{C}\:\:\:\:\:\:\:\:\:\:\:\:\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}=\frac{\pi}{\mathrm{4}}\int_{\mathrm{1}} ^{\infty} \frac{{dt}}{{t}^{\mathrm{2}} }=\frac{\pi}{\mathrm{4}} \\ $$$$\underset{{z}\rightarrow\infty} {\mathrm{lim}}{I}\left({z}\right)=−\frac{\pi}{\mathrm{4}}+{C}=\frac{\pi}{\mathrm{4}}\Rightarrow{C}=\frac{\pi}{\mathrm{2}} \\ $$$${I}\left({a}\right)=\pi{log}\left({a}+\mathrm{1}\right)+\frac{\pi}{\mathrm{4}}\Rightarrow{I}\left(\mathrm{2}\right)=\pi{log}\left(\mathrm{3}\right)+\frac{\pi}{\mathrm{4}} \\ $$
