Question Number 73182 by mathmax by abdo last updated on 07/Nov/19
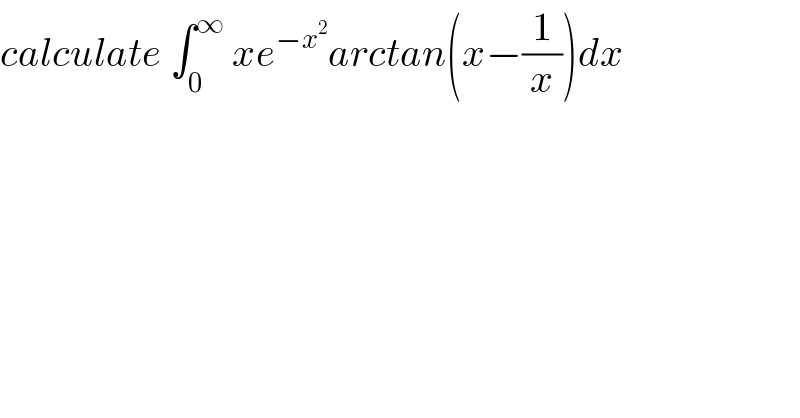
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:{xe}^{−{x}^{\mathrm{2}} } {arctan}\left({x}−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$
Commented by mathmax by abdo last updated on 08/Nov/19
![let A =∫_0 ^∞ x e^(−x^2 ) arctan(x−(1/x))dx by parts u^′ =xe^(−x^2 ) and v =arctan(x−(1/x)) ⇒ A =[−(1/2)e^(−x^2 ) arctan(x−(1/x))]_0 ^(+∞) −∫_0 ^∞ (−(1/2)e^(−x^2 ) )×((1+(1/x^2 ))/(1+(x−(1/x))^2 ))dx =−(π/4) +(1/2)∫_0 ^∞ (((x^2 +1)e^(−x^2 ) )/(x^2 {1+(((x^2 −1)^2 )/x^2 )}))dx =−(π/4) +(1/2)∫_0 ^∞ (((x^2 +1)e^(−x^2 ) )/(x^2 +(x^2 −1)^2 )) =−(π/4) +(1/2)∫_0 ^∞ (((x^2 +1)e^(−x^2 ) )/(+x^4 −x^2 +1))dx we have ∫_0 ^∞ (((x^2 +1)e^(−x^2 ) )/(x^4 −x^2 +1))dx =(1/2)∫_(−∞) ^(+∞) (((x^2 +)e^(−x^2 ) )/(x^4 −x^2 +1)) let ϕ(z)=(((z^2 +1)e^(−z^2 ) )/(z^4 −z^2 +1)) poles of ϕ? z^4 −z^2 +1 =0 ⇒t^2 −t +1=0 (t=z^2 ) Δ=1−4=−3 ⇒t_1 =((1+i(√3))/2) =e^((iπ)/3) and t_2 =((1−i(√3))/2) =e^(−((iπ)/3)) z^4 −z^2 +1=(z^2 −e^((iπ)/3) )(z^2 −e^(−((iπ)/3)) ) ⇒ ϕ(z) =(((z^2 +1)e^(−z^2 ) )/((z^2 −e^((iπ)/3) )(z^2 −e^(−((iπ)/3)) ))) =(((z^2 +1)e^(−z^2 ) )/((z−e^((iπ)/6) )(z+e^((iπ)/6) )(z−e^(−((iπ)/6)) )(z+e^(−((iπ)/6)) ))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,e^((iπ)/6) )+Res(ϕ,−e^(−((iπ)/6)) )}](https://www.tinkutara.com/question/Q73219.png)
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:\:{x}\:{e}^{−{x}^{\mathrm{2}} } \:{arctan}\left({x}−\frac{\mathrm{1}}{{x}}\right){dx}\:\:{by}\:{parts}\:{u}^{'} ={xe}^{−{x}^{\mathrm{2}} } \:{and} \\ $$$${v}\:={arctan}\left({x}−\frac{\mathrm{1}}{{x}}\right)\:\Rightarrow \\ $$$${A}\:=\left[−\frac{\mathrm{1}}{\mathrm{2}}{e}^{−{x}^{\mathrm{2}} } \:{arctan}\left({x}−\frac{\mathrm{1}}{{x}}\right)\right]_{\mathrm{0}} ^{+\infty} \:−\int_{\mathrm{0}} ^{\infty} \:\left(−\frac{\mathrm{1}}{\mathrm{2}}{e}^{−{x}^{\mathrm{2}} } \right)×\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{1}+\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} }{dx} \\ $$$$=−\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right){e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} \left\{\mathrm{1}+\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right\}}{dx} \\ $$$$=−\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} \:+\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:=−\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{x}^{\mathrm{2}} } }{+{x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{1}}{dx} \\ $$$${we}\:{have}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\:\frac{\left({x}^{\mathrm{2}} \:+\right){e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${let}\:\varphi\left({z}\right)=\frac{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{z}^{\mathrm{2}} } }{{z}^{\mathrm{4}} −{z}^{\mathrm{2}} \:+\mathrm{1}}\:{poles}\:{of}\:\varphi? \\ $$$${z}^{\mathrm{4}} −{z}^{\mathrm{2}} \:+\mathrm{1}\:=\mathrm{0}\:\Rightarrow{t}^{\mathrm{2}} −{t}\:+\mathrm{1}=\mathrm{0}\:\:\left({t}={z}^{\mathrm{2}} \right) \\ $$$$\Delta=\mathrm{1}−\mathrm{4}=−\mathrm{3}\:\Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{\frac{{i}\pi}{\mathrm{3}}} \:\:\:{and}\:\:{t}_{\mathrm{2}} =\frac{\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{−\frac{{i}\pi}{\mathrm{3}}} \\ $$$${z}^{\mathrm{4}} −{z}^{\mathrm{2}} \:+\mathrm{1}=\left({z}^{\mathrm{2}} −{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}^{\mathrm{2}} −{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\:\Rightarrow \\ $$$$\varphi\left({z}\right)\:=\frac{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{z}^{\mathrm{2}} } }{\left({z}^{\mathrm{2}} −{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}^{\mathrm{2}} −{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)} \\ $$$$=\frac{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{z}^{\mathrm{2}} } }{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)\right\} \\ $$$$ \\ $$
Commented by mind is power last updated on 08/Nov/19

$$\mathrm{you}\:\mathrm{miss}\:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{in}\:\mathrm{lign}\:\mathrm{4} \\ $$
Commented by mathmax by abdo last updated on 08/Nov/19

$${Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)\:=\frac{\left(\mathrm{1}+{e}^{\frac{{i}\pi}{\mathrm{3}}} \right){e}^{−{e}^{\frac{{i}\pi}{\mathrm{3}}} } }{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{6}}} \left({e}^{\frac{{i}\pi}{\mathrm{3}}} −{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\frac{{i}\pi}{\mathrm{6}}} ×\frac{\left(\mathrm{1}+{e}^{\frac{{i}\pi}{\mathrm{3}}} \right){e}^{−{e}^{\frac{{i}\pi}{\mathrm{3}}} } }{\mathrm{2}{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\left(\:{e}^{−\frac{{i}\pi}{\mathrm{6}}} \:+{e}^{\frac{{i}\pi}{\mathrm{6}}} \right){e}^{−{e}^{\frac{{i}\pi}{\mathrm{3}}} \:} \:=\frac{\mathrm{2}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{e}^{−{e}^{\frac{{i}\pi}{\mathrm{3}}} } }{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:=\frac{{e}^{−{e}^{\frac{{i}\pi}{\mathrm{3}}} } }{\mathrm{2}{i}} \\ $$$${Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)\:=\frac{\left(\mathrm{1}+{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\:{e}^{−{e}^{−\frac{{i}\pi}{\mathrm{3}}} } }{\left(−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)\left({e}^{−\frac{{i}\pi}{\mathrm{3}}} −{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)} \\ $$$$=\frac{{e}^{\frac{{i}\pi}{\mathrm{6}}} \left(\mathrm{1}+{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right){e}^{−{e}^{−\frac{{i}\pi}{\mathrm{3}}} } }{\mathrm{2}\left(\mathrm{2}{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}\:=\frac{\mathrm{2}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{e}^{−{e}^{−\frac{{i}\pi}{\mathrm{3}}} } }{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:=\frac{{e}^{−{e}^{−\frac{{i}\pi}{\mathrm{3}}} } }{\mathrm{2}{i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\frac{{e}^{−{e}^{\frac{{i}\pi}{\mathrm{3}}} } }{\mathrm{2}{i}}\:+\frac{{e}^{−{e}^{−\frac{{i}\pi}{\mathrm{3}}} } }{\mathrm{2}{i}}\right\} \\ $$$$=\pi\left\{\:{e}^{−{cos}\left(\frac{\pi}{\mathrm{3}}\right)−{isin}\left(\frac{\pi}{\mathrm{3}}\right)} \:\:+{e}^{−{cos}\left(\frac{\pi}{\mathrm{3}}\right)+{isin}\left(\frac{\pi}{\mathrm{3}}\right)} \right\} \\ $$$$=\pi\left\{\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}}−{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \:\:+{e}^{−\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \right\} \\ $$$$=\pi\left\{{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\:{e}^{\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}} \:+{e}^{−\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}} \right)\right\}\:=\frac{\pi}{\:\sqrt{{e}}}\:\left(\mathrm{2}\:{Re}\left({e}^{\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}} \right)\right) \\ $$$${e}^{\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}} \:={cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+{isin}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:\Rightarrow\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\frac{\mathrm{2}\pi}{\:\sqrt{{e}}}\:{cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$${A}\:=−\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{2}\pi}{\:\sqrt{{e}}}\:{cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:\Rightarrow\:{A}\:=\frac{\pi}{\mathrm{2}\sqrt{{e}}}\:{cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)−\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
