Question Number 143081 by Mathspace last updated on 09/Jun/21
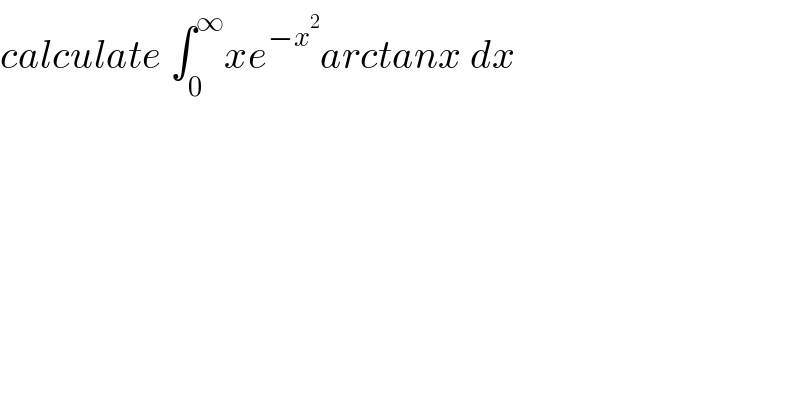
$${calculate}\:\int_{\mathrm{0}} ^{\infty} {xe}^{−{x}^{\mathrm{2}} } {arctanx}\:{dx} \\ $$
Answered by qaz last updated on 10/Jun/21
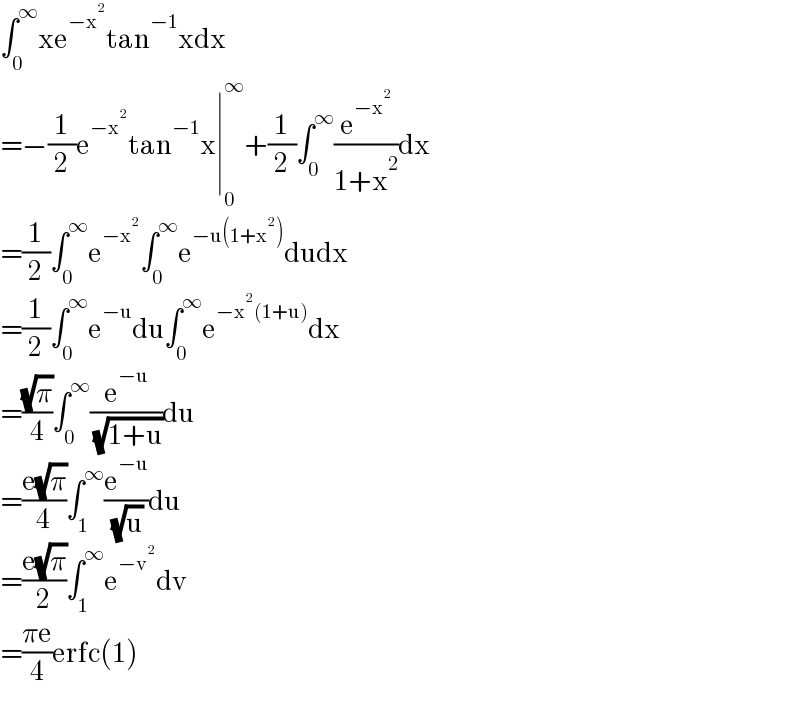
$$\int_{\mathrm{0}} ^{\infty} \mathrm{xe}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{tan}^{−\mathrm{1}} \mathrm{xdx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{tan}^{−\mathrm{1}} \mathrm{x}\mid_{\mathrm{0}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{u}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)} \mathrm{dudx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{u}} \mathrm{du}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{u}\right)} \mathrm{dx} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{−\mathrm{u}} }{\:\sqrt{\mathrm{1}+\mathrm{u}}}\mathrm{du} \\ $$$$=\frac{\mathrm{e}\sqrt{\pi}}{\mathrm{4}}\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{e}^{−\mathrm{u}} }{\:\sqrt{\mathrm{u}}}\mathrm{du} \\ $$$$=\frac{\mathrm{e}\sqrt{\pi}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \mathrm{e}^{−\mathrm{v}^{\mathrm{2}} } \mathrm{dv} \\ $$$$=\frac{\pi\mathrm{e}}{\mathrm{4}}\mathrm{erfc}\left(\mathrm{1}\right) \\ $$
Answered by mathmax by abdo last updated on 10/Jun/21
![Ψ=∫_0 ^∞ xe^(−x^2 ) arctanx dx by parts we get Ψ=[−(1/2)e^(−x^2 ) arctanx]_0 ^∞ +∫_0 ^∞ (1/2)e^(−x^2 ) (dx/(1+x^2 )) =(1/2)∫_0 ^∞ (e^(−x^2 ) /(1+x^2 ))dx ⇒2Ψ=∫_0 ^∞ (∫_0 ^∞ e^(−(1+x^2 )t) dt)e^(−x^2 ) dx =∫_0 ^∞ (∫_0 ^∞ e^(−(t+1)x^2 ) dx)e^(−t) dt =_((√(t+1))x=y) ∫_0 ^∞ (∫_1 ^∞ e^(−y^2 ) (dy/( (√(t+1)))))e^(−t) dt =∫_1 ^∞ e^(−y^2 ) dy ∫_0 ^∞ (e^(−t) /( (√(t+1))))dt =_(t+1=z^2 ) ∫_1 ^∞ e^(−y^2 ) dy.∫_1 ^∞ (e^(−(z^2 −1)) /z)(2z)dz =2e (∫_1 ^∞ e^(−y^2 ) dy)^2 if we put λ(1)=∫_1 ^∞ e^(−y^2 ) dy we get Ψ=2eλ^2 (1)](https://www.tinkutara.com/question/Q143143.png)
$$\Psi=\int_{\mathrm{0}} ^{\infty} \:\mathrm{xe}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{arctanx}\:\mathrm{dx}\:\mathrm{by}\:\mathrm{parts}\:\mathrm{we}\:\mathrm{get} \\ $$$$\Psi=\left[−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{arctanx}\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\mathrm{2}\Psi=\int_{\mathrm{0}} ^{\infty} \left(\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{t}} \mathrm{dt}\right)\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{t}+\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\right)\mathrm{e}^{−\mathrm{t}} \mathrm{dt}\:\: \\ $$$$=_{\sqrt{\mathrm{t}+\mathrm{1}}\mathrm{x}=\mathrm{y}} \:\:\:\int_{\mathrm{0}} ^{\infty} \left(\int_{\mathrm{1}} ^{\infty} \:\mathrm{e}^{−\mathrm{y}^{\mathrm{2}} } \frac{\mathrm{dy}}{\:\sqrt{\mathrm{t}+\mathrm{1}}}\right)\mathrm{e}^{−\mathrm{t}} \mathrm{dt} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \:\mathrm{e}^{−\mathrm{y}^{\mathrm{2}} } \mathrm{dy}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{t}} }{\:\sqrt{\mathrm{t}+\mathrm{1}}}\mathrm{dt} \\ $$$$=_{\mathrm{t}+\mathrm{1}=\mathrm{z}^{\mathrm{2}} } \:\:\:\int_{\mathrm{1}} ^{\infty} \:\mathrm{e}^{−\mathrm{y}^{\mathrm{2}} } \mathrm{dy}.\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{e}^{−\left(\mathrm{z}^{\mathrm{2}} −\mathrm{1}\right)} }{\mathrm{z}}\left(\mathrm{2z}\right)\mathrm{dz} \\ $$$$=\mathrm{2e}\:\left(\int_{\mathrm{1}} ^{\infty} \mathrm{e}^{−\mathrm{y}^{\mathrm{2}} } \mathrm{dy}\right)^{\mathrm{2}} \:\:\:\mathrm{if}\:\mathrm{we}\:\mathrm{put}\:\lambda\left(\mathrm{1}\right)=\int_{\mathrm{1}} ^{\infty} \:\mathrm{e}^{−\mathrm{y}^{\mathrm{2}} } \mathrm{dy}\:\mathrm{we}\:\mathrm{get} \\ $$$$\Psi=\mathrm{2e}\lambda^{\mathrm{2}} \left(\mathrm{1}\right)\: \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 10/Jun/21
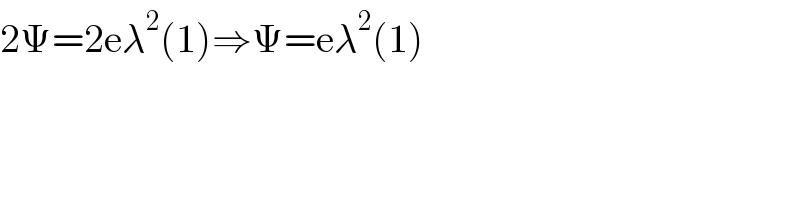
$$\mathrm{2}\Psi=\mathrm{2e}\lambda^{\mathrm{2}} \left(\mathrm{1}\right)\Rightarrow\Psi=\mathrm{e}\lambda^{\mathrm{2}} \left(\mathrm{1}\right) \\ $$
