Question Number 67038 by mathmax by abdo last updated on 22/Aug/19
$${calculate}\:\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{{x}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{{sinx}} }{dx}\:\:\:{with}\:{n}\:{integr}. \\ $$
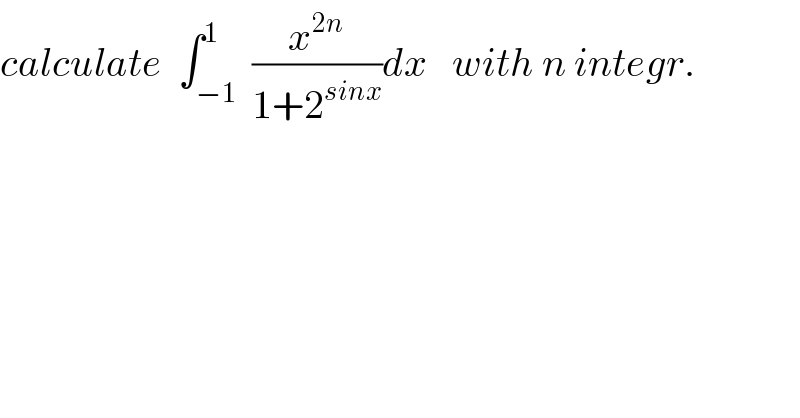
Commented by mathmax by abdo last updated on 22/Aug/19
![let A_n =∫_(−1) ^1 (x^(2n) /(1+2^(sinx) ))dx ⇒ A_n =∫_(−1) ^0 (x^(2n) /(1+2^(sinx) ))dx +∫_0 ^1 (x^(2n) /(1+2^(sinx) ))dx but ∫_(−1) ^0 (x^(2n) /(1+2^(sinx) ))dx =_(x=−t) ∫_0 ^1 (t^(2n) /(1+2^(−sint) ))dt =∫_0 ^1 ((2^(sint) t^(2n) )/(2^(sint) +1))dt ⇒ A_n =∫_0 ^1 (((2^(sint) t^(2n) )/(1+2^(sint) )) +(t^(2n) /(1+2^(sint) )))dt =∫_0 ^1 t^(2n) (((1+2^(sint) )/(1+2^(sint) )))dt =∫_0 ^1 t^(2n) dt [(t^(2n+1) /(2n+1))]_0 ^1 =(1/(2n+1)) ⇒ ★A_n =(1/(2n+1)) ★](https://www.tinkutara.com/question/Q67077.png)
$${let}\:{A}_{{n}} =\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{{x}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{{sinx}} }{dx}\:\Rightarrow\:{A}_{{n}} =\int_{−\mathrm{1}} ^{\mathrm{0}} \:\frac{{x}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{{sinx}} }{dx}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{{sinx}} }{dx}\:{but} \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{0}} \:\frac{{x}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{{sinx}} }{dx}\:=_{{x}=−{t}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{−{sint}} }{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}^{{sint}} \:{t}^{\mathrm{2}{n}} }{\mathrm{2}^{{sint}} \:+\mathrm{1}}{dt}\:\Rightarrow \\ $$$${A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\left(\frac{\mathrm{2}^{{sint}} \:{t}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{{sint}} }\:+\frac{{t}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{{sint}} }\right){dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}{n}} \left(\frac{\mathrm{1}+\mathrm{2}^{{sint}} }{\mathrm{1}+\mathrm{2}^{{sint}} }\right){dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{\mathrm{2}{n}} \:{dt} \\ $$$$\left[\frac{{t}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:\Rightarrow\:\bigstar{A}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:\bigstar \\ $$
Answered by mind is power last updated on 22/Aug/19
$$\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{{sin}\left({x}\right)} }{dx}=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\left(−{x}\right)^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{{sin}\left(−{x}\right)} }{dx}=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{−{sin}\left({x}\right)} }{dx}=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{2}^{{sin}\left({x}\right)} {x}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{{son}\left({x}\right)} } \\ $$$$==>\mathrm{2}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{{sin}\left({x}\right)} }\:{dx}=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{{sin}\left({x}\right)} }{dx}+\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}{n}} \mathrm{2}^{{sin}\left({x}\left\{\right.\right.} }{\mathrm{1}+\mathrm{2}^{{sin}\left({x}\right)} }{dx}=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}{n}} +{x}^{\mathrm{2}{n}} \mathrm{2}^{{sin}\left({x}\right)} \:\:}{\mathrm{1}+\mathrm{2}^{{sin}\left({x}\right)} }=\int_{−\mathrm{1}} ^{\mathrm{1}} {x}^{\mathrm{2}{n}} {dx}=\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=>\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}{n}} }{\mathrm{1}+\mathrm{2}^{{sin}\left({x}\right)} }{dx}=\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}} \\ $$
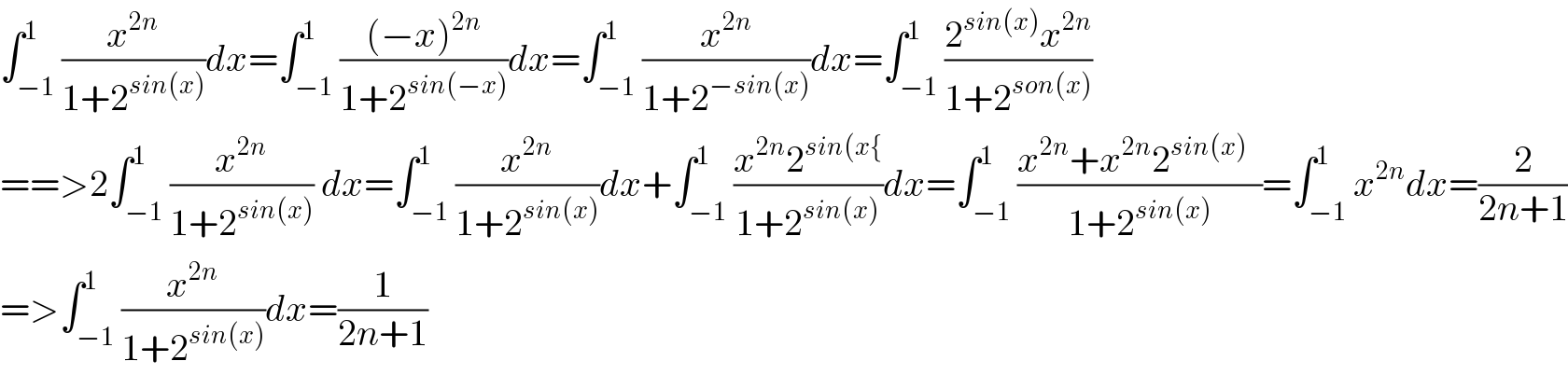
Commented by mathmax by abdo last updated on 22/Aug/19
$${thank}\:{you}\:{sir}. \\ $$
Commented by mind is power last updated on 23/Aug/19
$${y}'{re}\:{welcom} \\ $$