Menu Close

calculate-1-cos-1-i-sin-1-3i-2-arctan-i-arctan-2i-arctan-1-i-arctan-1-i-arctan-1-2i-3-have-us-conj-arctanz-arctan-z-

Tinku Tara 0 Comments
Pin




Question Number 73411 by mathmax by abdo last updated on 11/Nov/19
calculate 1)cos(1+i) , sin(1+3i) 2) arctan(i), arctan(2i) , arctan(1+i) ,arctan(1−i) , arctan(1+2i). 3) have us conj(arctanz)=arctan(z^− )?
$${calculate}\:\: \\ $$$$\left.\mathrm{1}\right){cos}\left(\mathrm{1}+{i}\right)\:,\:{sin}\left(\mathrm{1}+\mathrm{3}{i}\right) \\ $$$$\left.\mathrm{2}\right)\:{arctan}\left({i}\right),\:{arctan}\left(\mathrm{2}{i}\right)\:,\:{arctan}\left(\mathrm{1}+{i}\right)\:,{arctan}\left(\mathrm{1}−{i}\right)\:, \\ $$$${arctan}\left(\mathrm{1}+\mathrm{2}{i}\right). \\ $$$$\left.\mathrm{3}\right)\:{have}\:{us}\:\:{conj}\left({arctanz}\right)={arctan}\left(\overset{−} {{z}}\right)? \\ $$
Commented by mathmax by abdo last updated on 12/Nov/19
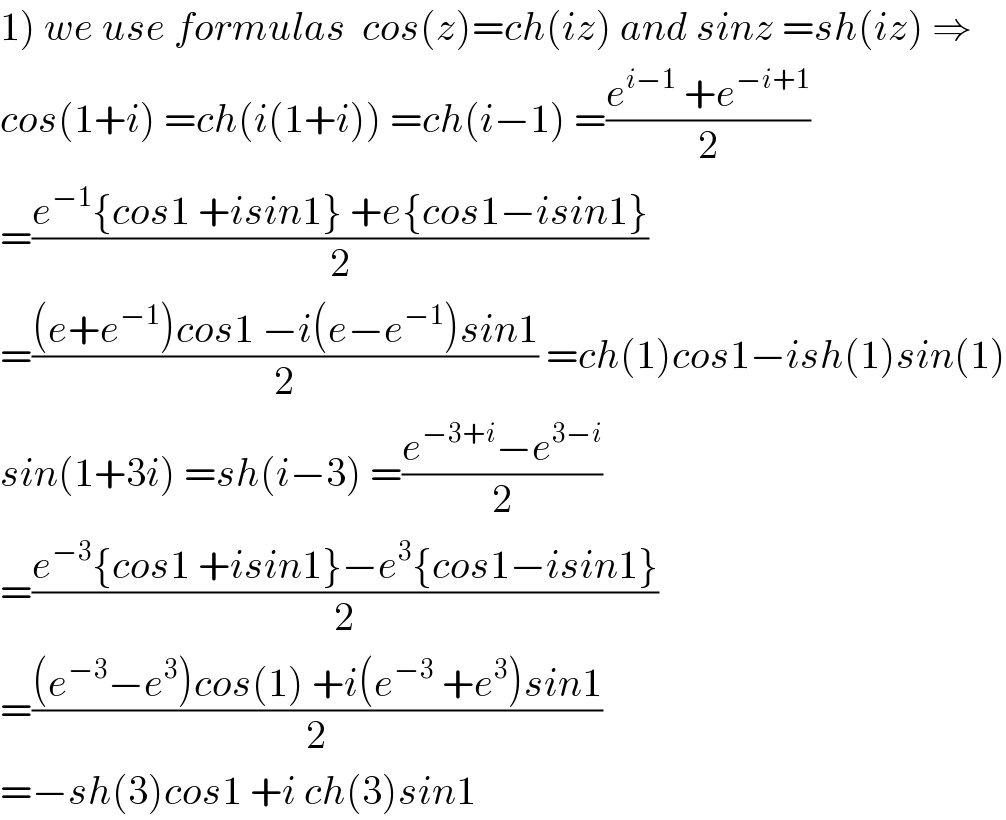
1) we use formulas cos(z)=ch(iz) and sinz =sh(iz) ⇒ cos(1+i) =ch(i(1+i)) =ch(i−1) =((e^(i−1) +e^(−i+1) )/2) =((e^(−1) {cos1 +isin1} +e{cos1−isin1})/2) =(((e+e^(−1) )cos1 −i(e−e^(−1) )sin1)/2) =ch(1)cos1−ish(1)sin(1) sin(1+3i) =sh(i−3) =((e^(−3+i) −e^(3−i) )/2) =((e^(−3) {cos1 +isin1}−e^3 {cos1−isin1})/2) =(((e^(−3) −e^3 )cos(1) +i(e^(−3) +e^3 )sin1)/2) =−sh(3)cos1 +i ch(3)sin1
$$\left.\mathrm{1}\right)\:{we}\:{use}\:{formulas}\:\:{cos}\left({z}\right)={ch}\left({iz}\right)\:{and}\:{sinz}\:={sh}\left({iz}\right)\:\Rightarrow \\ $$$${cos}\left(\mathrm{1}+{i}\right)\:={ch}\left({i}\left(\mathrm{1}+{i}\right)\right)\:={ch}\left({i}−\mathrm{1}\right)\:=\frac{{e}^{{i}−\mathrm{1}} \:+{e}^{−{i}+\mathrm{1}} }{\mathrm{2}} \\ $$$$=\frac{{e}^{−\mathrm{1}} \left\{{cos}\mathrm{1}\:+{isin}\mathrm{1}\right\}\:+{e}\left\{{cos}\mathrm{1}−{isin}\mathrm{1}\right\}}{\mathrm{2}} \\ $$$$=\frac{\left({e}+{e}^{−\mathrm{1}} \right){cos}\mathrm{1}\:−{i}\left({e}−{e}^{−\mathrm{1}} \right){sin}\mathrm{1}}{\mathrm{2}}\:={ch}\left(\mathrm{1}\right){cos}\mathrm{1}−{ish}\left(\mathrm{1}\right){sin}\left(\mathrm{1}\right) \\ $$$${sin}\left(\mathrm{1}+\mathrm{3}{i}\right)\:={sh}\left({i}−\mathrm{3}\right)\:=\frac{{e}^{−\mathrm{3}+{i}} −{e}^{\mathrm{3}−{i}} }{\mathrm{2}} \\ $$$$=\frac{{e}^{−\mathrm{3}} \left\{{cos}\mathrm{1}\:+{isin}\mathrm{1}\right\}−{e}^{\mathrm{3}} \left\{{cos}\mathrm{1}−{isin}\mathrm{1}\right\}}{\mathrm{2}} \\ $$$$=\frac{\left({e}^{−\mathrm{3}} −{e}^{\mathrm{3}} \right){cos}\left(\mathrm{1}\right)\:+{i}\left({e}^{−\mathrm{3}} \:+{e}^{\mathrm{3}} \right){sin}\mathrm{1}}{\mathrm{2}} \\ $$$$=−{sh}\left(\mathrm{3}\right){cos}\mathrm{1}\:+{i}\:{ch}\left(\mathrm{3}\right){sin}\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 12/Nov/19
2) we have arctan(z)=(1/(2i))ln(((1+iz)/(1−iz))) ⇒ arctan(i)can not calculed by this formula arctan(2i) =(1/(2i))ln(((1+i(2i))/(1−i(2i))))=(1/(2i))ln(((−1)/3)) =(1/(2i))ln(−1)+(1/(2i))ln((1/3)) =(1/(2i))(iπ)−(1/(2i))ln(3) =(π/2) +(i/2)ln(3) arctan(1+i) =(1/(2i))ln(((1+i(1+i))/(1−i(1+i)))) =(1/(2i))ln(((1+i−1)/(1−i +1))) =(1/(2i))ln((i/(2−i))) =(1/(2i)){ln(i)−ln(2−i)} =(1/(2i)){ ((iπ)/2)−ln((√5)e^(−i arctan((1/2))) } =(π/4) −(1/(2i))(ln((√5)) −i arctan((1/2))) =(π/4) +(i/4)ln(5) +(1/2) arctan((1/2))=(π/4) +(1/2) arctan((1/2))+((ln(5))/4)i arctan(1−i) =(1/(2i))ln(((1+i(1−i))/(1−i(1−i)))) =(1/(2i))ln(((1+i+1)/(1−i−1))) =(1/(2i))ln(((2+i)/(−i))) =(1/(2i)){ln(2+i)−ln(−i)} =(1/(2i)){ ln((√5)e^(iarctan((1/2))) +(((iπ)/2))} =(1/(2i))ln((√5))+(1/(2i))(iarctan((1/2))) +(π/4) =−(i/4)ln(5) +(1/2) arctan((1/2))+(π/4) =(π/4) +(1/2) arctan((1/2))−((ln(5))/4)i we see that conj(arctan(1+i))=arctan(conj(1+i)) rest to prove this result in general case. arctan(1+2i) =(1/(2i))ln(((1+i(1+2i))/(1−i(1+2i)))) =(1/(2i))ln( ((1+i−2)/(1−i+2))) =(1/(2i))ln(((−1+i)/(3−i))) =(1/(2i)){ ln(−1+i)−ln(3−i)} =(1/(2i)){ ln((√2)e^(−iarctan(1)) )−ln((√(10))e^(−i arctan((1/3))) )} =(1/(2i)){ ln((√2))−i(π/4)−ln((√(10))) +i arctan((1/3))} =−(i/4)ln(2)+(i/4)ln(10) −(π/8) +(1/2) arctan((1/3)) =(i/4)ln(5) +(1/2)arctan((1/3))−((ln(2))/4) i don t forget the formula arctanz =(1/(2i))ln(((1+iz)/(1−iz))) z from C
$$\left.\mathrm{2}\right)\:\:{we}\:{have}\:{arctan}\left({z}\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{iz}}{\mathrm{1}−{iz}}\right)\:\Rightarrow\:{arctan}\left({i}\right){can}\:{not}\: \\ $$$${calculed}\:{by}\:{this}\:{formula} \\ $$$${arctan}\left(\mathrm{2}{i}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{i}\left(\mathrm{2}{i}\right)}{\mathrm{1}−{i}\left(\mathrm{2}{i}\right)}\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{−\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}\left({i}\pi\right)−\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\mathrm{3}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}\:+\frac{{i}}{\mathrm{2}}{ln}\left(\mathrm{3}\right) \\ $$$${arctan}\left(\mathrm{1}+{i}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{i}\left(\mathrm{1}+{i}\right)}{\mathrm{1}−{i}\left(\mathrm{1}+{i}\right)}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{i}−\mathrm{1}}{\mathrm{1}−{i}\:+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{{i}}{\mathrm{2}−{i}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{{ln}\left({i}\right)−{ln}\left(\mathrm{2}−{i}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\:\frac{{i}\pi}{\mathrm{2}}−{ln}\left(\sqrt{\mathrm{5}}{e}^{−{i}\:{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \right\}\right. \\ $$$$=\frac{\pi}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{2}{i}}\left({ln}\left(\sqrt{\mathrm{5}}\right)\:−{i}\:{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$=\frac{\pi}{\mathrm{4}}\:+\frac{{i}}{\mathrm{4}}{ln}\left(\mathrm{5}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{{ln}\left(\mathrm{5}\right)}{\mathrm{4}}{i} \\ $$$${arctan}\left(\mathrm{1}−{i}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{i}\left(\mathrm{1}−{i}\right)}{\mathrm{1}−{i}\left(\mathrm{1}−{i}\right)}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{i}+\mathrm{1}}{\mathrm{1}−{i}−\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{2}+{i}}{−{i}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{{ln}\left(\mathrm{2}+{i}\right)−{ln}\left(−{i}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\:{ln}\left(\sqrt{\mathrm{5}}{e}^{{iarctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} +\left(\frac{{i}\pi}{\mathrm{2}}\right)\right\}\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\sqrt{\mathrm{5}}\right)+\frac{\mathrm{1}}{\mathrm{2}{i}}\left({iarctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\right. \\ $$$$+\frac{\pi}{\mathrm{4}}\:=−\frac{{i}}{\mathrm{4}}{ln}\left(\mathrm{5}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\pi}{\mathrm{4}} \\ $$$$=\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{{ln}\left(\mathrm{5}\right)}{\mathrm{4}}{i}\:\:{we}\:{see}\:{that} \\ $$$${conj}\left({arctan}\left(\mathrm{1}+{i}\right)\right)={arctan}\left({conj}\left(\mathrm{1}+{i}\right)\right)\:{rest}\:{to}\:{prove}\:{this}\:{result} \\ $$$${in}\:{general}\:{case}. \\ $$$${arctan}\left(\mathrm{1}+\mathrm{2}{i}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{i}\left(\mathrm{1}+\mathrm{2}{i}\right)}{\mathrm{1}−{i}\left(\mathrm{1}+\mathrm{2}{i}\right)}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\:\frac{\mathrm{1}+{i}−\mathrm{2}}{\mathrm{1}−{i}+\mathrm{2}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{−\mathrm{1}+{i}}{\mathrm{3}−{i}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\:{ln}\left(−\mathrm{1}+{i}\right)−{ln}\left(\mathrm{3}−{i}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\:{ln}\left(\sqrt{\mathrm{2}}{e}^{−{iarctan}\left(\mathrm{1}\right)} \right)−{ln}\left(\sqrt{\mathrm{10}}{e}^{−{i}\:{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)} \right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\:{ln}\left(\sqrt{\mathrm{2}}\right)−{i}\frac{\pi}{\mathrm{4}}−{ln}\left(\sqrt{\mathrm{10}}\right)\:+{i}\:{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right\} \\ $$$$=−\frac{{i}}{\mathrm{4}}{ln}\left(\mathrm{2}\right)+\frac{{i}}{\mathrm{4}}{ln}\left(\mathrm{10}\right)\:−\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\frac{{i}}{\mathrm{4}}{ln}\left(\mathrm{5}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{4}}\:{i} \\ $$$${don}\:{t}\:{forget}\:{the}\:{formula} \\ $$$${arctanz}\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{iz}}{\mathrm{1}−{iz}}\right)\:\:{z}\:{from}\:{C} \\ $$$$ \\ $$
Answered by MJS last updated on 11/Nov/19
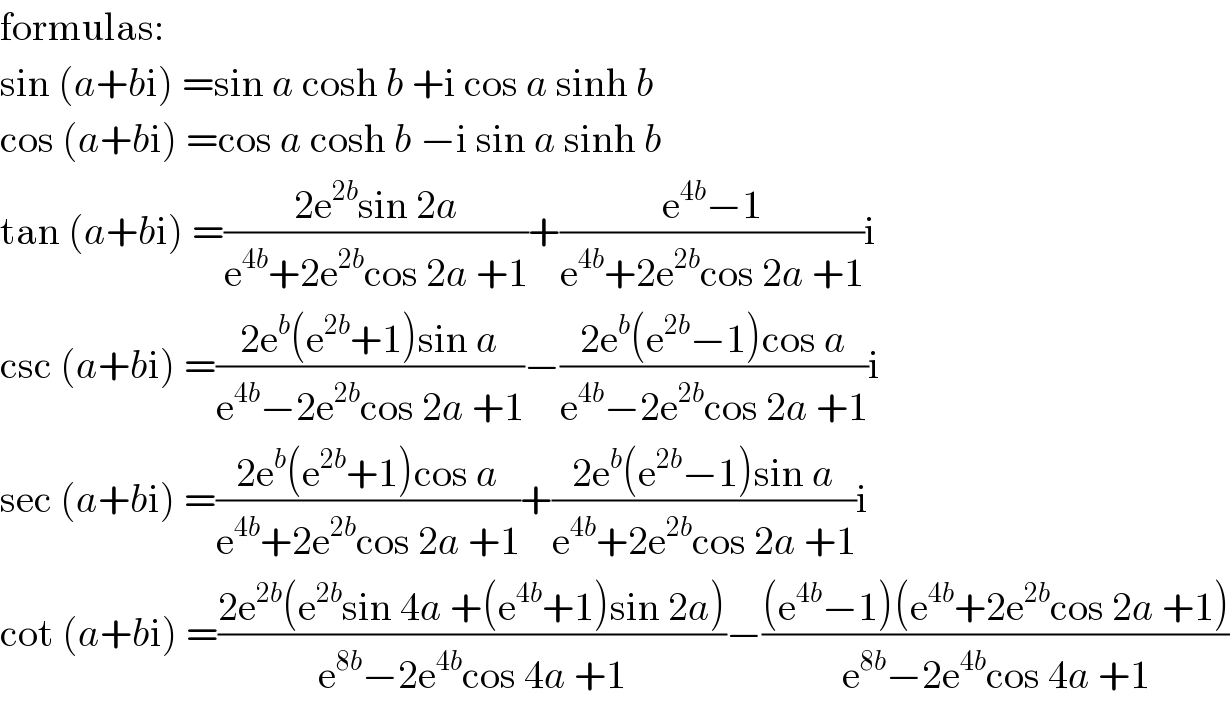
formulas: sin (a+bi) =sin a cosh b +i cos a sinh b cos (a+bi) =cos a cosh b −i sin a sinh b tan (a+bi) =((2e^(2b) sin 2a)/(e^(4b) +2e^(2b) cos 2a +1))+((e^(4b) −1)/(e^(4b) +2e^(2b) cos 2a +1))i csc (a+bi) =((2e^b (e^(2b) +1)sin a)/(e^(4b) −2e^(2b) cos 2a +1))−((2e^b (e^(2b) −1)cos a)/(e^(4b) −2e^(2b) cos 2a +1))i sec (a+bi) =((2e^b (e^(2b) +1)cos a)/(e^(4b) +2e^(2b) cos 2a +1))+((2e^b (e^(2b) −1)sin a)/(e^(4b) +2e^(2b) cos 2a +1))i cot (a+bi) =((2e^(2b) (e^(2b) sin 4a +(e^(4b) +1)sin 2a))/(e^(8b) −2e^(4b) cos 4a +1))−(((e^(4b) −1)(e^(4b) +2e^(2b) cos 2a +1))/(e^(8b) −2e^(4b) cos 4a +1))
$$\mathrm{formulas}: \\ $$$$\mathrm{sin}\:\left({a}+{b}\mathrm{i}\right)\:=\mathrm{sin}\:{a}\:\mathrm{cosh}\:{b}\:+\mathrm{i}\:\mathrm{cos}\:{a}\:\mathrm{sinh}\:{b} \\ $$$$\mathrm{cos}\:\left({a}+{b}\mathrm{i}\right)\:=\mathrm{cos}\:{a}\:\mathrm{cosh}\:{b}\:−\mathrm{i}\:\mathrm{sin}\:{a}\:\mathrm{sinh}\:{b} \\ $$$$\mathrm{tan}\:\left({a}+{b}\mathrm{i}\right)\:=\frac{\mathrm{2e}^{\mathrm{2}{b}} \mathrm{sin}\:\mathrm{2}{a}}{\mathrm{e}^{\mathrm{4}{b}} +\mathrm{2e}^{\mathrm{2}{b}} \mathrm{cos}\:\mathrm{2}{a}\:+\mathrm{1}}+\frac{\mathrm{e}^{\mathrm{4}{b}} −\mathrm{1}}{\mathrm{e}^{\mathrm{4}{b}} +\mathrm{2e}^{\mathrm{2}{b}} \mathrm{cos}\:\mathrm{2}{a}\:+\mathrm{1}}\mathrm{i} \\ $$$$\mathrm{csc}\:\left({a}+{b}\mathrm{i}\right)\:=\frac{\mathrm{2e}^{{b}} \left(\mathrm{e}^{\mathrm{2}{b}} +\mathrm{1}\right)\mathrm{sin}\:{a}}{\mathrm{e}^{\mathrm{4}{b}} −\mathrm{2e}^{\mathrm{2}{b}} \mathrm{cos}\:\mathrm{2}{a}\:+\mathrm{1}}−\frac{\mathrm{2e}^{{b}} \left(\mathrm{e}^{\mathrm{2}{b}} −\mathrm{1}\right)\mathrm{cos}\:{a}}{\mathrm{e}^{\mathrm{4}{b}} −\mathrm{2e}^{\mathrm{2}{b}} \mathrm{cos}\:\mathrm{2}{a}\:+\mathrm{1}}\mathrm{i} \\ $$$$\mathrm{sec}\:\left({a}+{b}\mathrm{i}\right)\:=\frac{\mathrm{2e}^{{b}} \left(\mathrm{e}^{\mathrm{2}{b}} +\mathrm{1}\right)\mathrm{cos}\:{a}}{\mathrm{e}^{\mathrm{4}{b}} +\mathrm{2e}^{\mathrm{2}{b}} \mathrm{cos}\:\mathrm{2}{a}\:+\mathrm{1}}+\frac{\mathrm{2e}^{{b}} \left(\mathrm{e}^{\mathrm{2}{b}} −\mathrm{1}\right)\mathrm{sin}\:{a}}{\mathrm{e}^{\mathrm{4}{b}} +\mathrm{2e}^{\mathrm{2}{b}} \mathrm{cos}\:\mathrm{2}{a}\:+\mathrm{1}}\mathrm{i} \\ $$$$\mathrm{cot}\:\left({a}+{b}\mathrm{i}\right)\:=\frac{\mathrm{2e}^{\mathrm{2}{b}} \left(\mathrm{e}^{\mathrm{2}{b}} \mathrm{sin}\:\mathrm{4}{a}\:+\left(\mathrm{e}^{\mathrm{4}{b}} +\mathrm{1}\right)\mathrm{sin}\:\mathrm{2}{a}\right)}{\mathrm{e}^{\mathrm{8}{b}} −\mathrm{2e}^{\mathrm{4}{b}} \mathrm{cos}\:\mathrm{4}{a}\:+\mathrm{1}}−\frac{\left(\mathrm{e}^{\mathrm{4}{b}} −\mathrm{1}\right)\left(\mathrm{e}^{\mathrm{4}{b}} +\mathrm{2e}^{\mathrm{2}{b}} \mathrm{cos}\:\mathrm{2}{a}\:+\mathrm{1}\right)}{\mathrm{e}^{\mathrm{8}{b}} −\mathrm{2e}^{\mathrm{4}{b}} \mathrm{cos}\:\mathrm{4}{a}\:+\mathrm{1}} \\ $$
Answered by MJS last updated on 12/Nov/19
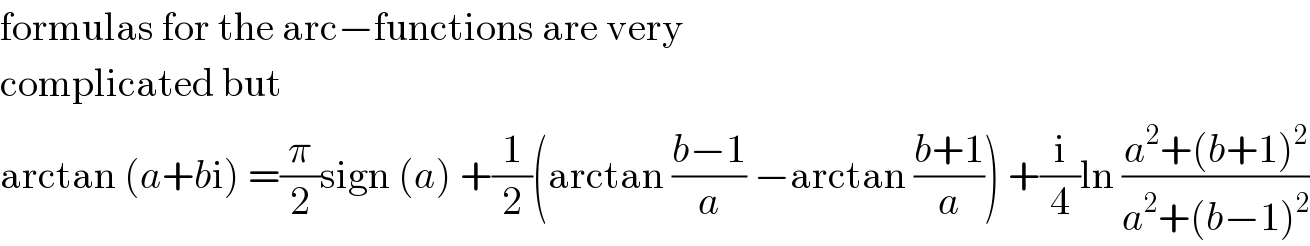
formulas for the arc−functions are very complicated but arctan (a+bi) =(π/2)sign (a) +(1/2)(arctan ((b−1)/a) −arctan ((b+1)/a)) +(i/4)ln ((a^2 +(b+1)^2 )/(a^2 +(b−1)^2 ))
$$\mathrm{formulas}\:\mathrm{for}\:\mathrm{the}\:\mathrm{arc}−\mathrm{functions}\:\mathrm{are}\:\mathrm{very} \\ $$$$\mathrm{complicated}\:\mathrm{but} \\ $$$$\mathrm{arctan}\:\left({a}+{b}\mathrm{i}\right)\:=\frac{\pi}{\mathrm{2}}\mathrm{sign}\:\left({a}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{arctan}\:\frac{{b}−\mathrm{1}}{{a}}\:−\mathrm{arctan}\:\frac{{b}+\mathrm{1}}{{a}}\right)\:+\frac{\mathrm{i}}{\mathrm{4}}\mathrm{ln}\:\frac{{a}^{\mathrm{2}} +\left({b}+\mathrm{1}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} +\left({b}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *