Question Number 142365 by mathmax by abdo last updated on 30/May/21
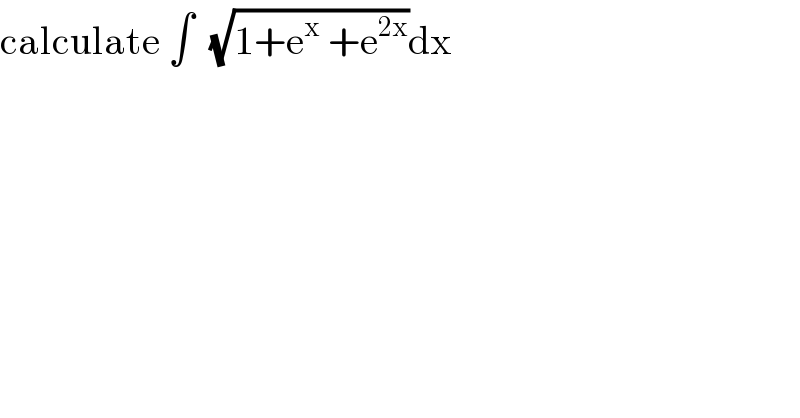
$$\mathrm{calculate}\:\int\:\:\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} \:+\mathrm{e}^{\mathrm{2x}} }\mathrm{dx} \\ $$
Answered by MJS_new last updated on 05/Jun/21
![∫(√(e^(2x) +e^x +1))dx= [t=e^x +(1/2) → dx=(dt/e^x )] =∫((√(4t^2 +3))/(2t−1))dt= [u=((2t+(√(4t^2 +3)))/( (√3))) → dt=((√(4t^2 +3))/(2u))du] =((3(√3))/4)∫(((u^2 +1)^2 )/(u^2 (u−(√3))(3u+(√3))))du= =∫(((√3)/4)−((√3)/(4u^2 ))+(1/(2u))+(1/(u−(√3)))−(3/(3u+(√3))))du= =(((√3)u)/4)+((√3)/(4u))+((ln u)/2)+ln (u−(√3)) −ln (3u+(√3)) = =(((√3)(u^2 +1))/(4u))+(1/2)ln ((u(u−(√3))^2 )/((3u+(√3))^2 )) = ... =(√(e^(2x) +e^x +1))−x+(1/2)ln (2e^(3x) −3e^(2x) −8+2(e^(2x) −2e^x +4)(√(e^(2x) +e^x +1))) +C](https://www.tinkutara.com/question/Q142792.png)
$$\int\sqrt{\mathrm{e}^{\mathrm{2}{x}} +\mathrm{e}^{{x}} +\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{e}^{{x}} +\frac{\mathrm{1}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{e}^{{x}} }\right] \\ $$$$=\int\frac{\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}}}{\mathrm{2}{t}−\mathrm{1}}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\mathrm{2}{t}+\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}}}{\:\sqrt{\mathrm{3}}}\:\rightarrow\:{dt}=\frac{\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}}}{\mathrm{2}{u}}{du}\right] \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}}\int\frac{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{{u}^{\mathrm{2}} \left({u}−\sqrt{\mathrm{3}}\right)\left(\mathrm{3}{u}+\sqrt{\mathrm{3}}\right)}{du}= \\ $$$$=\int\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}{u}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}{u}}+\frac{\mathrm{1}}{{u}−\sqrt{\mathrm{3}}}−\frac{\mathrm{3}}{\mathrm{3}{u}+\sqrt{\mathrm{3}}}\right){du}= \\ $$$$=\frac{\sqrt{\mathrm{3}}{u}}{\mathrm{4}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{4}{u}}+\frac{\mathrm{ln}\:{u}}{\mathrm{2}}+\mathrm{ln}\:\left({u}−\sqrt{\mathrm{3}}\right)\:−\mathrm{ln}\:\left(\mathrm{3}{u}+\sqrt{\mathrm{3}}\right)\:= \\ $$$$=\frac{\sqrt{\mathrm{3}}\left({u}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{4}{u}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{{u}\left({u}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }{\left(\mathrm{3}{u}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\:= \\ $$$$… \\ $$$$=\sqrt{\mathrm{e}^{\mathrm{2}{x}} +\mathrm{e}^{{x}} +\mathrm{1}}−{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2e}^{\mathrm{3}{x}} −\mathrm{3e}^{\mathrm{2}{x}} −\mathrm{8}+\mathrm{2}\left(\mathrm{e}^{\mathrm{2}{x}} −\mathrm{2e}^{{x}} +\mathrm{4}\right)\sqrt{\mathrm{e}^{\mathrm{2}{x}} +\mathrm{e}^{{x}} +\mathrm{1}}\right)\:+{C} \\ $$
