Menu Close

Calculate-1-I-c-zdz-z-1-2-z-2-2z-1-2i-C-z-z-2-2-J-c-ch-z-dz-z-e-z-1-C-z-z-3i-4-3-K-c-sin-z-dz-z-3-z-1-2-C-z-z-2-

Tinku Tara
Pin




Question Number 131094 by Chhing last updated on 01/Feb/21
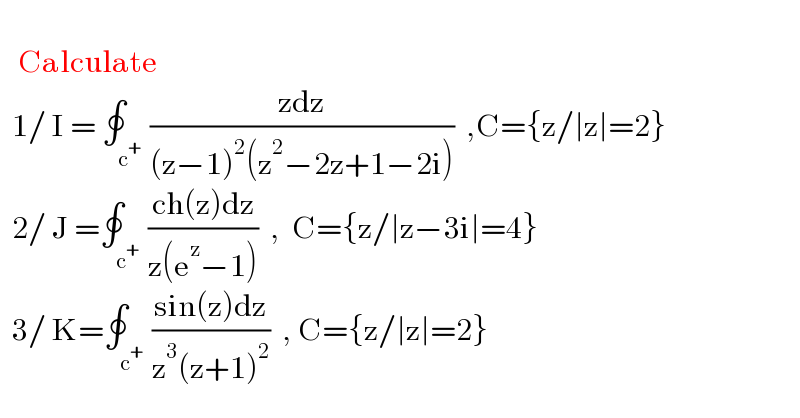
Calculate 1/ I = ∮_c^+ ((zdz)/((z−1)^2 (z^2 −2z+1−2i))) ,C={z/∣z∣=2} 2/ J =∮_c^+ ((ch(z)dz)/(z(e^z −1))) , C={z/∣z−3i∣=4} 3/ K=∮_c^+ ((sin(z)dz)/(z^3 (z+1)^2 )) , C={z/∣z∣=2}
$$\:\: \\ $$$$\:\:\:\mathrm{Calculate} \\ $$$$\:\:\mathrm{1}/\:\mathrm{I}\:=\:\oint_{\mathrm{c}^{+} } \frac{\mathrm{zdz}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{z}^{\mathrm{2}} −\mathrm{2z}+\mathrm{1}−\mathrm{2i}\right)}\:\:,\mathrm{C}=\left\{\mathrm{z}/\mid\mathrm{z}\mid=\mathrm{2}\right\}\: \\ $$$$\:\:\mathrm{2}/\:\mathrm{J}\:=\oint_{\mathrm{c}^{+} } \frac{\mathrm{ch}\left(\mathrm{z}\right)\mathrm{dz}}{\mathrm{z}\left(\mathrm{e}^{\mathrm{z}} −\mathrm{1}\right)}\:\:,\:\:\mathrm{C}=\left\{\mathrm{z}/\mid\mathrm{z}−\mathrm{3i}\mid=\mathrm{4}\right\} \\ $$$$\:\:\mathrm{3}/\:\mathrm{K}=\oint_{\mathrm{c}^{+} } \frac{\mathrm{sin}\left(\mathrm{z}\right)\mathrm{dz}}{\mathrm{z}^{\mathrm{3}} \left(\mathrm{z}+\mathrm{1}\right)^{\mathrm{2}} }\:\:,\:\mathrm{C}=\left\{\mathrm{z}/\mid\mathrm{z}\mid=\mathrm{2}\right\} \\ $$
Commented by mathmax by abdo last updated on 02/Feb/21
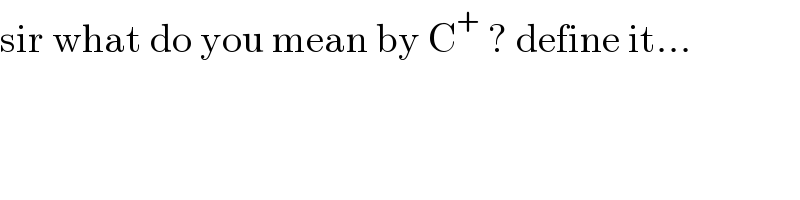
sir what do you mean by C^+ ? define it...
$$\mathrm{sir}\:\mathrm{what}\:\mathrm{do}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{by}\:\mathrm{C}^{+} \:?\:\mathrm{define}\:\mathrm{it}… \\ $$
Answered by mathmax by abdo last updated on 01/Feb/21
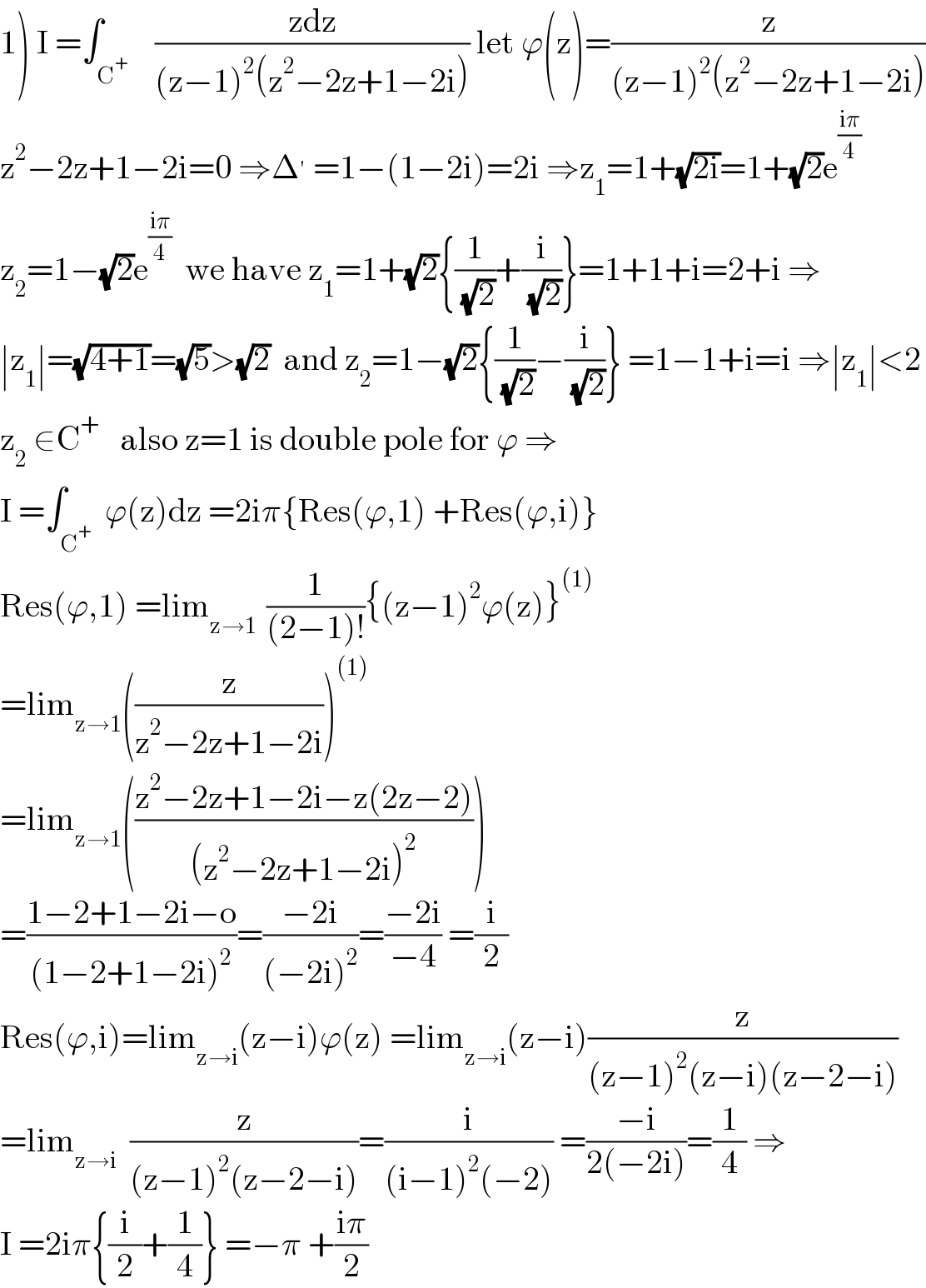
1) I =∫_C^+ ((zdz)/((z−1)^2 (z^2 −2z+1−2i))) let ϕ(z)=(z/((z−1)^2 (z^2 −2z+1−2i))) z^2 −2z+1−2i=0 ⇒Δ^′ =1−(1−2i)=2i ⇒z_1 =1+(√(2i))=1+(√2)e^((iπ)/4) z_2 =1−(√2)e^((iπ)/4) we have z_1 =1+(√2){(1/( (√2)))+(i/( (√2)))}=1+1+i=2+i ⇒ ∣z_1 ∣=(√(4+1))=(√5)>(√2) and z_2 =1−(√2){(1/( (√2)))−(i/( (√2)))} =1−1+i=i ⇒∣z_1 ∣<2 z_2 ∈C^+ also z=1 is double pole for ϕ ⇒ I =∫_C^+ ϕ(z)dz =2iπ{Res(ϕ,1) +Res(ϕ,i)} Res(ϕ,1) =lim_(z→1 ) (1/((2−1)!)){(z−1)^2 ϕ(z)}^((1)) =lim_(z→1) ((z/(z^2 −2z+1−2i)))^((1)) =lim_(z→1) (((z^2 −2z+1−2i−z(2z−2))/((z^2 −2z+1−2i)^2 ))) =((1−2+1−2i−o)/((1−2+1−2i)^2 ))=((−2i)/((−2i)^2 ))=((−2i)/(−4)) =(i/2) Res(ϕ,i)=lim_(z→i) (z−i)ϕ(z) =lim_(z→i) (z−i)(z/((z−1)^2 (z−i)(z−2−i))) =lim_(z→i) (z/((z−1)^2 (z−2−i)))=(i/((i−1)^2 (−2))) =((−i)/(2(−2i)))=(1/4) ⇒ I =2iπ{(i/2)+(1/4)} =−π +((iπ)/2)
$$\left.\mathrm{1}\right)\:\mathrm{I}\:=\int_{\mathrm{C}^{+} } \:\:\:\frac{\mathrm{zdz}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{z}^{\mathrm{2}} −\mathrm{2z}+\mathrm{1}−\mathrm{2i}\right)}\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{z}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{z}^{\mathrm{2}} −\mathrm{2z}+\mathrm{1}−\mathrm{2i}\right)} \\ $$$$\mathrm{z}^{\mathrm{2}} −\mathrm{2z}+\mathrm{1}−\mathrm{2i}=\mathrm{0}\:\Rightarrow\Delta^{'} \:=\mathrm{1}−\left(\mathrm{1}−\mathrm{2i}\right)=\mathrm{2i}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{2i}}=\mathrm{1}+\sqrt{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \\ $$$$\mathrm{z}_{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \:\:\mathrm{we}\:\mathrm{have}\:\mathrm{z}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{2}}\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\right\}=\mathrm{1}+\mathrm{1}+\mathrm{i}=\mathrm{2}+\mathrm{i}\:\Rightarrow \\ $$$$\mid\mathrm{z}_{\mathrm{1}} \mid=\sqrt{\mathrm{4}+\mathrm{1}}=\sqrt{\mathrm{5}}>\sqrt{\mathrm{2}}\:\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{2}}\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\right\}\:=\mathrm{1}−\mathrm{1}+\mathrm{i}=\mathrm{i}\:\Rightarrow\mid\mathrm{z}_{\mathrm{1}} \mid<\mathrm{2} \\ $$$$\mathrm{z}_{\mathrm{2}} \:\in\mathrm{C}^{+} \:\:\:\mathrm{also}\:\mathrm{z}=\mathrm{1}\:\mathrm{is}\:\mathrm{double}\:\mathrm{pole}\:\mathrm{for}\:\varphi\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{C}^{+} } \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\mathrm{Res}\left(\varphi,\mathrm{1}\right)\:+\mathrm{Res}\left(\varphi,\mathrm{i}\right)\right\} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{1}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{1}\:} \:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{1}} \left(\frac{\mathrm{z}}{\mathrm{z}^{\mathrm{2}} −\mathrm{2z}+\mathrm{1}−\mathrm{2i}}\right)^{\left(\mathrm{1}\right)} \: \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{1}} \left(\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{2z}+\mathrm{1}−\mathrm{2i}−\mathrm{z}\left(\mathrm{2z}−\mathrm{2}\right)}{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{2z}+\mathrm{1}−\mathrm{2i}\right)^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}−\mathrm{2}+\mathrm{1}−\mathrm{2i}−\mathrm{o}}{\left(\mathrm{1}−\mathrm{2}+\mathrm{1}−\mathrm{2i}\right)^{\mathrm{2}} }=\frac{−\mathrm{2i}}{\left(−\mathrm{2i}\right)^{\mathrm{2}} }=\frac{−\mathrm{2i}}{−\mathrm{4}}\:=\frac{\mathrm{i}}{\mathrm{2}} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{i}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \left(\mathrm{z}−\mathrm{i}\right)\varphi\left(\mathrm{z}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \left(\mathrm{z}−\mathrm{i}\right)\frac{\mathrm{z}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{z}−\mathrm{i}\right)\left(\mathrm{z}−\mathrm{2}−\mathrm{i}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\frac{\mathrm{z}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{z}−\mathrm{2}−\mathrm{i}\right)}=\frac{\mathrm{i}}{\left(\mathrm{i}−\mathrm{1}\right)^{\mathrm{2}} \left(−\mathrm{2}\right)}\:=\frac{−\mathrm{i}}{\mathrm{2}\left(−\mathrm{2i}\right)}=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{2i}\pi\left\{\frac{\mathrm{i}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right\}\:=−\pi\:+\frac{\mathrm{i}\pi}{\mathrm{2}} \\ $$

Pin