Menu Close

calculate-3x-1-x-2-4-x-3-2x-3-dx-

Tinku Tara
Pin




Question Number 65678 by mathmax by abdo last updated on 01/Aug/19
calculate ∫ ((3x+1)/((x^2 −4)(x^3 +2x−3)))dx
$${calculate}\:\:\int\:\:\:\:\frac{\mathrm{3}{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{4}\right)\left({x}^{\mathrm{3}} +\mathrm{2}{x}−\mathrm{3}\right)}{dx} \\ $$
Commented by mathmax by abdo last updated on 03/Aug/19
let I =∫ ((3x+1)/((x^2 −4)(x^3 +2x−3))) let decompose F(x)=((3x+1)/((x^2 −4)(x^3 +2x−3))) we have x^3 +2x−3 =x^3 −1 +2x−2 =(x−1)(x^2 +x+1)+2(x−1) =(x−1)(x^2 +x+3) ⇒F(x) =((3x+1)/((x−2)(x+2)(x−1)(x^2 +x+3))) =(a/(x−2)) +(b/(x+2)) +(c/((x−1))) +((dx+e)/(x^2 +x+3)) a =lim_(x→2) (x−2)F(x) =(7/(4.9)) =(7/(36)) b =lm_(x→−2) (x+2)F(x)=((−5)/((−4)(−3)(5))) =−(1/(12)) c =lim_(x→1) (x−1)F(x) =(4/((−1)(3)(3))) =−(4/9) lim_(x→+∞) xF(x) =0 =a+b+c +d ⇒d =−a−b−c =−(7/(36)) +(1/(12)) +(4/9) =((−7+3+16)/(36)) =((12)/(36)) =(1/3) F(0) =(1/((−2)(2)(−1)3)) =(1/(12)) =−(a/2) +(b/2)−c +(e/3) ⇒ 1 =−6a +6b−12c +4e ⇒4e =1+6a−6b+12c =1+(7/6) +(1/2) −((4.3.4)/(3.3)) =(3/2) +(7/6)−((16)/3) =((9+7−32)/6) =((16−32)/6) =((−16)/6) =−(8/3) ⇒F(x)=(7/(36(x−2))) −(1/(12(x+2)))−(4/(9(x−1))) +(((1/3)x−(2/3))/(x^2 +x+3)) ⇒ I =∫ F(x)dx =(7/(36))ln∣x−2∣−(1/(12))ln∣x+2∣−(4/9)ln∣x−1∣ +(1/3) ∫ ((x−2)/(x^2 +x+3))dx +c and ∫((x−2)/(x^2 +x+3)) =(1/2)∫ ((2x+1−5)/(x^2 +x+3)) =(1/2)ln(x^2 +x+3)−(5/2)∫ (dx/(x^2 +x+3)) ∫ (dx/(x^2 +x+3)) =∫ (dx/(x^2 +2(x/2)+(1/4) +3−(1/4))) =∫ (dx/((x+(1/2))^2 +((11)/4))) =_(x+(1/2)=((√(11))/2)u) (4/(11)) ∫ (1/(1+u^2 )) ((√(11))/2)du =(2/( (√(11)))) arctan(((2x+1)/( (√(11))))) the value of I is known...
$${let}\:{I}\:=\int\:\:\frac{\mathrm{3}{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{4}\right)\left({x}^{\mathrm{3}} \:+\mathrm{2}{x}−\mathrm{3}\right)}\:{let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{3}{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{4}\right)\left({x}^{\mathrm{3}} \:+\mathrm{2}{x}−\mathrm{3}\right)} \\ $$$${we}\:{have}\:{x}^{\mathrm{3}} \:+\mathrm{2}{x}−\mathrm{3}\:={x}^{\mathrm{3}} −\mathrm{1}\:+\mathrm{2}{x}−\mathrm{2}\:=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)+\mathrm{2}\left({x}−\mathrm{1}\right) \\ $$$$=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+{x}+\mathrm{3}\right)\:\Rightarrow{F}\left({x}\right)\:=\frac{\mathrm{3}{x}+\mathrm{1}}{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{2}\right)\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+{x}+\mathrm{3}\right)} \\ $$$$=\frac{{a}}{{x}−\mathrm{2}}\:+\frac{{b}}{{x}+\mathrm{2}}\:+\frac{{c}}{\left({x}−\mathrm{1}\right)}\:+\frac{{dx}+{e}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{3}} \\ $$$${a}\:={lim}_{{x}\rightarrow\mathrm{2}} \left({x}−\mathrm{2}\right){F}\left({x}\right)\:=\frac{\mathrm{7}}{\mathrm{4}.\mathrm{9}}\:=\frac{\mathrm{7}}{\mathrm{36}} \\ $$$${b}\:={lm}_{{x}\rightarrow−\mathrm{2}} \left({x}+\mathrm{2}\right){F}\left({x}\right)=\frac{−\mathrm{5}}{\left(−\mathrm{4}\right)\left(−\mathrm{3}\right)\left(\mathrm{5}\right)}\:=−\frac{\mathrm{1}}{\mathrm{12}} \\ $$$${c}\:={lim}_{{x}\rightarrow\mathrm{1}} \left({x}−\mathrm{1}\right){F}\left({x}\right)\:=\frac{\mathrm{4}}{\left(−\mathrm{1}\right)\left(\mathrm{3}\right)\left(\mathrm{3}\right)}\:=−\frac{\mathrm{4}}{\mathrm{9}} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)\:=\mathrm{0}\:={a}+{b}+{c}\:+{d}\:\Rightarrow{d}\:=−{a}−{b}−{c}\:=−\frac{\mathrm{7}}{\mathrm{36}}\:+\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$+\frac{\mathrm{4}}{\mathrm{9}}\:=\frac{−\mathrm{7}+\mathrm{3}+\mathrm{16}}{\mathrm{36}}\:=\frac{\mathrm{12}}{\mathrm{36}}\:=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${F}\left(\mathrm{0}\right)\:=\frac{\mathrm{1}}{\left(−\mathrm{2}\right)\left(\mathrm{2}\right)\left(−\mathrm{1}\right)\mathrm{3}}\:=\frac{\mathrm{1}}{\mathrm{12}}\:=−\frac{{a}}{\mathrm{2}}\:+\frac{{b}}{\mathrm{2}}−{c}\:+\frac{{e}}{\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{1}\:=−\mathrm{6}{a}\:+\mathrm{6}{b}−\mathrm{12}{c}\:+\mathrm{4}{e}\:\Rightarrow\mathrm{4}{e}\:=\mathrm{1}+\mathrm{6}{a}−\mathrm{6}{b}+\mathrm{12}{c} \\ $$$$=\mathrm{1}+\frac{\mathrm{7}}{\mathrm{6}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{4}.\mathrm{3}.\mathrm{4}}{\mathrm{3}.\mathrm{3}}\:=\frac{\mathrm{3}}{\mathrm{2}}\:+\frac{\mathrm{7}}{\mathrm{6}}−\frac{\mathrm{16}}{\mathrm{3}}\:=\frac{\mathrm{9}+\mathrm{7}−\mathrm{32}}{\mathrm{6}}\:=\frac{\mathrm{16}−\mathrm{32}}{\mathrm{6}}\:=\frac{−\mathrm{16}}{\mathrm{6}}\:=−\frac{\mathrm{8}}{\mathrm{3}} \\ $$$$\Rightarrow{F}\left({x}\right)=\frac{\mathrm{7}}{\mathrm{36}\left({x}−\mathrm{2}\right)}\:−\frac{\mathrm{1}}{\mathrm{12}\left({x}+\mathrm{2}\right)}−\frac{\mathrm{4}}{\mathrm{9}\left({x}−\mathrm{1}\right)}\:+\frac{\frac{\mathrm{1}}{\mathrm{3}}{x}−\frac{\mathrm{2}}{\mathrm{3}}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{3}}\:\Rightarrow \\ $$$${I}\:=\int\:{F}\left({x}\right){dx}\:=\frac{\mathrm{7}}{\mathrm{36}}{ln}\mid{x}−\mathrm{2}\mid−\frac{\mathrm{1}}{\mathrm{12}}{ln}\mid{x}+\mathrm{2}\mid−\frac{\mathrm{4}}{\mathrm{9}}{ln}\mid{x}−\mathrm{1}\mid \\ $$$$+\frac{\mathrm{1}}{\mathrm{3}}\:\int\:\:\:\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{3}}{dx}\:+{c}\:{and} \\ $$$$\int\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{3}}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{2}{x}+\mathrm{1}−\mathrm{5}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{3}}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \:+{x}+\mathrm{3}\right)−\frac{\mathrm{5}}{\mathrm{2}}\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{3}} \\ $$$$\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{3}}\:=\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{2}\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\:+\mathrm{3}−\frac{\mathrm{1}}{\mathrm{4}}}\:=\int\:\:\:\frac{{dx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{11}}{\mathrm{4}}} \\ $$$$=_{{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}{u}} \:\:\:\:\:\frac{\mathrm{4}}{\mathrm{11}}\:\int\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}{du}\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{11}}}\:{arctan}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{11}}}\right) \\ $$$${the}\:{value}\:{of}\:\:{I}\:{is}\:{known}… \\ $$$$ \\ $$$$ \\ $$
Answered by Tanmay chaudhury last updated on 02/Aug/19
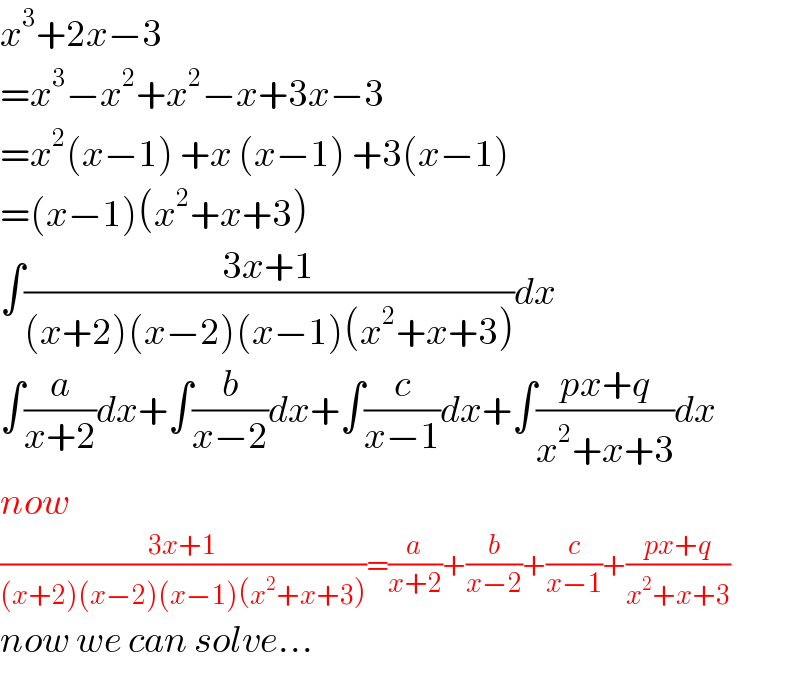
x^3 +2x−3 =x^3 −x^2 +x^2 −x+3x−3 =x^2 (x−1) +x (x−1) +3(x−1) =(x−1)(x^2 +x+3) ∫((3x+1)/((x+2)(x−2)(x−1)(x^2 +x+3)))dx ∫(a/(x+2))dx+∫(b/(x−2))dx+∫(c/(x−1))dx+∫((px+q)/(x^2 +x+3))dx now ((3x+1)/((x+2)(x−2)(x−1)(x^2 +x+3)))=(a/(x+2))+(b/(x−2))+(c/(x−1))+((px+q)/(x^2 +x+3)) now we can solve...
$${x}^{\mathrm{3}} +\mathrm{2}{x}−\mathrm{3} \\ $$$$={x}^{\mathrm{3}} −{x}^{\mathrm{2}} +{x}^{\mathrm{2}} −{x}+\mathrm{3}{x}−\mathrm{3} \\ $$$$={x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)\:+{x}\:\left({x}−\mathrm{1}\right)\:+\mathrm{3}\left({x}−\mathrm{1}\right) \\ $$$$=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{3}\right) \\ $$$$\int\frac{\mathrm{3}{x}+\mathrm{1}}{\left({x}+\mathrm{2}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{3}\right)}{dx} \\ $$$$\int\frac{{a}}{{x}+\mathrm{2}}{dx}+\int\frac{{b}}{{x}−\mathrm{2}}{dx}+\int\frac{{c}}{{x}−\mathrm{1}}{dx}+\int\frac{{px}+{q}}{{x}^{\mathrm{2}} +{x}+\mathrm{3}}{dx} \\ $$$${now} \\ $$$$\frac{\mathrm{3}{x}+\mathrm{1}}{\left({x}+\mathrm{2}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{3}\right)}=\frac{{a}}{{x}+\mathrm{2}}+\frac{{b}}{{x}−\mathrm{2}}+\frac{{c}}{{x}−\mathrm{1}}+\frac{{px}+{q}}{{x}^{\mathrm{2}} +{x}+\mathrm{3}} \\ $$$${now}\:{we}\:{can}\:{solve}… \\ $$

Pin