Menu Close

calculate-c-0-cos-x-1-x-4-dx-

Tinku Tara 0 Comments
Pin




Question Number 133213 by mathmax by abdo last updated on 20/Feb/21
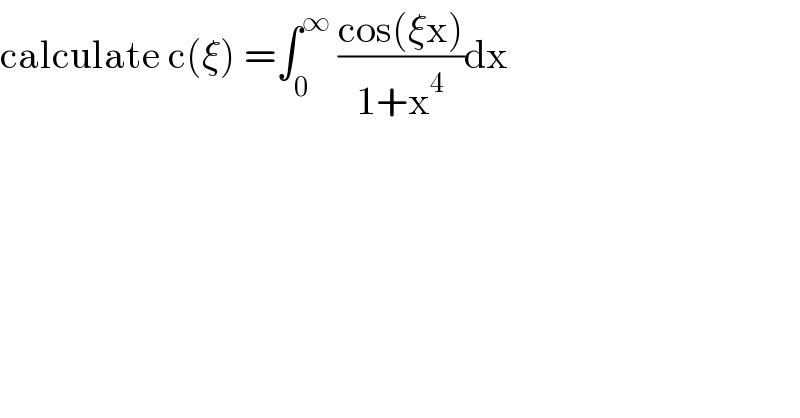
calculate c(ξ) =∫_0 ^∞ ((cos(ξx))/(1+x^4 ))dx
$$\mathrm{calculate}\:\mathrm{c}\left(\xi\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\xi\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 20/Feb/21
Φ(ξ)=∫_0 ^∞ ((cos(ξx))/(x^4 +1))dx ⇒2Φ(ξ)=∫_(−∞) ^(+∞) ((cos(ξx))/(x^4 +1))dx =Re(∫_(−∞) ^(+∞) (e^(iξx) /(x^4 +1))dx) let ϕ(z)=(e^(iξz) /(z^4 +1)) ⇒ϕ(z)=(e^(iξz) /((z^2 −i)(z^2 +i))) =(e^(iξz) /((z−(√i))(z+(√i))(z−(√(−i)))(z+(√(−i)))))=(e^(iξz) /((z−e^((iπ)/4) )(z+e^((iπ)/4) )(z−e^(−((iπ)/4)) )(z+e^(−((iπ)/4)) ))) and ∫_R ϕ(z)dz =2iπ{Res(ϕ,e^((iπ)/4) )+Res(ϕ,−e^(−((iπ)/4)) )} Res(ϕ,e^((iπ)/4) ) =(e^(iξe^((iπ)/4) ) /(2e^((iπ)/4) (2i))) =(1/(4i))e^(−((iπ)/4)) .e^(iξ((1/( (√2)))+(i/( (√2))))) =(1/(4i))e^(−((iπ)/4)) .e^((iξ)/( (√2))) .e^(−(ξ/( (√2)))) =(1/(4i))e^(−(ξ/( (√2)))) e^(i(−(π/4)+(ξ/( (√2))))) Res(ϕ,−e^(−((iπ)/4)) ) =(e^(−iξe^(−((iπ)/4)) ) /(−2e^(−((iπ)/4)) (−2i)))=(1/(4i))e^((iπ)/4) .e^(−iξ((1/( (√2)))−(i/( (√2))))) =(1/(4i)) e^((iπ)/4) .e^(−((iξ)/( (√2)))) .e^(−(ξ/( (√2)))) =(1/(4i)) e^(−(ξ/( (√2)))) e^(i((π/4)−(ξ/( (√2))))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ.(1/(4i))e^(−(ξ/( (√2)))) {e^(i(−(π/4)+(ξ/( (√2))))) +e^(i((π/4)−(ξ/( (√2))))) } =(π/2)e^(−(ξ/( (√2)))) { e^(i((π/4)−(ξ/( (√2))))) +e^(−i((π/4)−(ξ/( (√2))))) } =(π/2)e^(−(ξ/( (√2)))) {2cos((π/4)−(ξ/( (√2))))} =e^(−(ξ/( (√2)))) cos((π/4)−(ξ/( (√2))))=2Φ(ξ) ⇒ Φ(ξ)=(1/2)e^(−(ξ/( (√2)))) cos((π/4)−(ξ/( (√2))))
$$\Phi\left(\xi\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\xi\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}\mathrm{dx}\:\Rightarrow\mathrm{2}\Phi\left(\xi\right)=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\xi\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}\mathrm{dx} \\ $$$$=\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{i}\xi\mathrm{x}} }{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}\mathrm{dx}\right)\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\mathrm{i}\xi\mathrm{z}} }{\mathrm{z}^{\mathrm{4}} \:+\mathrm{1}}\:\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\mathrm{i}\xi\mathrm{z}} }{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{i}\right)\left(\mathrm{z}^{\mathrm{2}} +\mathrm{i}\right)} \\ $$$$=\frac{\mathrm{e}^{\mathrm{i}\xi\mathrm{z}} }{\left(\mathrm{z}−\sqrt{\mathrm{i}}\right)\left(\mathrm{z}+\sqrt{\mathrm{i}}\right)\left(\mathrm{z}−\sqrt{−\mathrm{i}}\right)\left(\mathrm{z}+\sqrt{−\mathrm{i}}\right)}=\frac{\mathrm{e}^{\mathrm{i}\xi\mathrm{z}} }{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{z}+\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)} \\ $$$$\mathrm{and}\:\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)+\mathrm{Res}\left(\varphi,−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\:=\frac{\mathrm{e}^{\mathrm{i}\xi\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} } }{\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \left(\mathrm{2i}\right)}\:=\frac{\mathrm{1}}{\mathrm{4i}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \:.\mathrm{e}^{\mathrm{i}\xi\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4i}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} .\mathrm{e}^{\frac{\mathrm{i}\xi}{\:\sqrt{\mathrm{2}}}} \:\:.\mathrm{e}^{−\frac{\xi}{\:\sqrt{\mathrm{2}}}} \:=\frac{\mathrm{1}}{\mathrm{4i}}\mathrm{e}^{−\frac{\xi}{\:\sqrt{\mathrm{2}}}} \:\mathrm{e}^{\mathrm{i}\left(−\frac{\pi}{\mathrm{4}}+\frac{\xi}{\:\sqrt{\mathrm{2}}}\right)} \\ $$$$\mathrm{Res}\left(\varphi,−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\:=\frac{\mathrm{e}^{−\mathrm{i}\xi\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} } }{−\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \left(−\mathrm{2i}\right)}=\frac{\mathrm{1}}{\mathrm{4i}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \:.\mathrm{e}^{−\mathrm{i}\xi\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4i}}\:\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} .\mathrm{e}^{−\frac{\mathrm{i}\xi}{\:\sqrt{\mathrm{2}}}} \:\:\:.\mathrm{e}^{−\frac{\xi}{\:\sqrt{\mathrm{2}}}} \:\:=\frac{\mathrm{1}}{\mathrm{4i}}\:\mathrm{e}^{−\frac{\xi}{\:\sqrt{\mathrm{2}}}} \:\:\:\:\mathrm{e}^{\mathrm{i}\left(\frac{\pi}{\mathrm{4}}−\frac{\xi}{\:\sqrt{\mathrm{2}}}\right)} \:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi.\frac{\mathrm{1}}{\mathrm{4i}}\mathrm{e}^{−\frac{\xi}{\:\sqrt{\mathrm{2}}}} \:\:\left\{\mathrm{e}^{\mathrm{i}\left(−\frac{\pi}{\mathrm{4}}+\frac{\xi}{\:\sqrt{\mathrm{2}}}\right)} \:+\mathrm{e}^{\mathrm{i}\left(\frac{\pi}{\mathrm{4}}−\frac{\xi}{\:\sqrt{\mathrm{2}}}\right)} \right\} \\ $$$$=\frac{\pi}{\mathrm{2}}\mathrm{e}^{−\frac{\xi}{\:\sqrt{\mathrm{2}}}} \:\:\left\{\:\mathrm{e}^{\mathrm{i}\left(\frac{\pi}{\mathrm{4}}−\frac{\xi}{\:\sqrt{\mathrm{2}}}\right)} \:+\mathrm{e}^{−\mathrm{i}\left(\frac{\pi}{\mathrm{4}}−\frac{\xi}{\:\sqrt{\mathrm{2}}}\right)} \right\} \\ $$$$=\frac{\pi}{\mathrm{2}}\mathrm{e}^{−\frac{\xi}{\:\sqrt{\mathrm{2}}}} \:\:\:\left\{\mathrm{2cos}\left(\frac{\pi}{\mathrm{4}}−\frac{\xi}{\:\sqrt{\mathrm{2}}}\right)\right\}\:=\mathrm{e}^{−\frac{\xi}{\:\sqrt{\mathrm{2}}}} \:\:\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−\frac{\xi}{\:\sqrt{\mathrm{2}}}\right)=\mathrm{2}\Phi\left(\xi\right)\:\Rightarrow \\ $$$$\Phi\left(\xi\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\frac{\xi}{\:\sqrt{\mathrm{2}}}} \:\:\:\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−\frac{\xi}{\:\sqrt{\mathrm{2}}}\right) \\ $$
Commented by mnjuly1970 last updated on 21/Feb/21
nice very nice sir Max..
$$\:{nice}\:{very}\:{nice}\:{sir}\:{Max}.. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *