Question Number 11900 by @ANTARES_VY last updated on 04/Apr/17
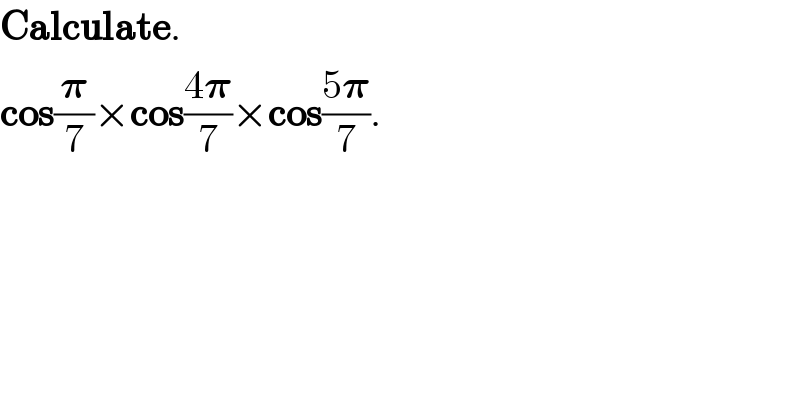
$$\boldsymbol{\mathrm{Calculate}}. \\ $$$$\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\pi}}{\mathrm{7}}×\boldsymbol{\mathrm{cos}}\frac{\mathrm{4}\boldsymbol{\pi}}{\mathrm{7}}×\boldsymbol{\mathrm{cos}}\frac{\mathrm{5}\boldsymbol{\pi}}{\mathrm{7}}. \\ $$
Answered by ajfour last updated on 04/Apr/17
![= cos (π/7)cos ((4π)/7)[−cos (π−((5π)/7)) ] = −cos (π/7)cos ((4π)/7)cos ((2π)/7) = ((−1)/(2sin (π/7)))[ 2sin (π/7)cos (π/7)][cos ((2π)/7)cos ((4π)/7) ] =−(1/(2sin (π/7)))[sin ((2π)/7)cos ((2π)/7)]cos ((4π)/7) = −(1/(4sin (π/7)))(sin ((4π)/7)cos ((4π)/7)) = −(((sin ((8π)/7))/(8sin (π/7))))= −((sin (π+(π/7)))/(8sin (π/7))) = −((−sin (π/7))/(8sin (π/7))) = (1/8) .](https://www.tinkutara.com/question/Q11904.png)
$$=\:\mathrm{cos}\:\frac{\pi}{\mathrm{7}}\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}}\left[−\mathrm{cos}\:\left(\pi−\frac{\mathrm{5}\pi}{\mathrm{7}}\right)\:\right] \\ $$$$=\:−\mathrm{cos}\:\frac{\pi}{\mathrm{7}}\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}}\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{7}} \\ $$$$=\:\frac{−\mathrm{1}}{\mathrm{2sin}\:\frac{\pi}{\mathrm{7}}}\left[\:\mathrm{2sin}\:\frac{\pi}{\mathrm{7}}\mathrm{cos}\:\frac{\pi}{\mathrm{7}}\right]\left[\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{7}}\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}}\:\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2sin}\:\frac{\pi}{\mathrm{7}}}\left[\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{7}}\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{7}}\right]\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}} \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{4sin}\:\frac{\pi}{\mathrm{7}}}\left(\mathrm{sin}\:\frac{\mathrm{4}\pi}{\mathrm{7}}\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}}\right) \\ $$$$=\:−\left(\frac{\mathrm{sin}\:\frac{\mathrm{8}\pi}{\mathrm{7}}}{\mathrm{8sin}\:\frac{\pi}{\mathrm{7}}}\right)=\:−\frac{\mathrm{sin}\:\left(\pi+\frac{\pi}{\mathrm{7}}\right)}{\mathrm{8sin}\:\frac{\pi}{\mathrm{7}}} \\ $$$$=\:−\frac{−\mathrm{sin}\:\left(\pi/\mathrm{7}\right)}{\mathrm{8sin}\:\left(\pi/\mathrm{7}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\:. \\ $$
