Menu Close

calculate-cos-e-x-e-x-x-2-x-1-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 77751 by abdomathmax last updated on 09/Jan/20
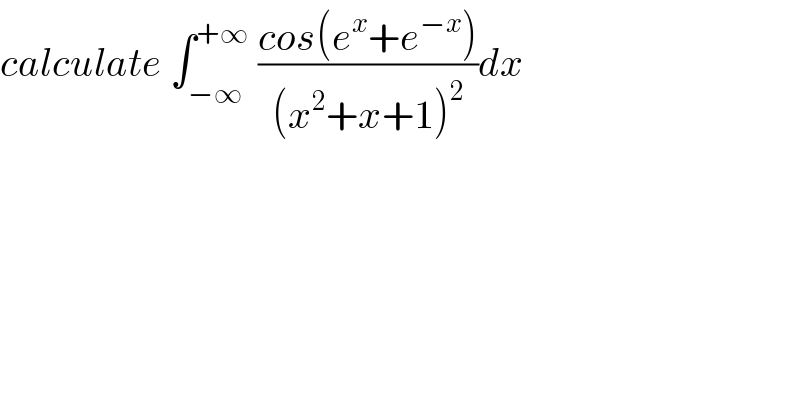
calculate ∫_(−∞) ^(+∞) ((cos(e^x +e^(−x) ))/((x^2 +x+1)^2 ))dx
$${calculate}\:\int_{−\infty} ^{+\infty} \:\frac{{cos}\left({e}^{{x}} +{e}^{−{x}} \right)}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$
Commented by msup trace by abdo last updated on 10/Jan/20
let I=∫_(−∞) ^(+∞) ((cos(e^x +e^(−x) ))/((x^2 +x+1)^2 )) dx ⇒ I=Re(∫_(−∞) ^(+∞) (e^(i(e^x +e^(−x) )) /((x^2 +x+1)^2 ))dx) let ϕ(z)=(e^(i(e^z +e^(−z) )) /((z^2 +z+1)^2 )) poles of ϕ? z^2 +z+1=0 →Δ=−3 ⇒ z_1 =((−1+i(√3))/2) =e^(i((2π)/3)) and z_2 =((−1−i(√3))/2) =e^(−((i2π)/3)) ⇒ϕ(z)=(e^(i(e^z +e^(−z) )) /((z−e^((i2π)/3) )^2 (z−e^(−((i2π)/3)) )^2 )) ∫_(−∞) ^(+∞) ϕ(z)dz = 2iπ{ Re(ϕ,e^((i2π)/3) )+Res(ϕ,e^(−((i2π)/3)) )} Res(ϕ,e^((i2π)/3) )=lim_(z→e^((i2π)/3) ) (1/((2−1)!)){(z−e^(i((2π)/3)) )ϕ(z)}^((1))
$${let}\:{I}=\int_{−\infty} ^{+\infty} \frac{{cos}\left({e}^{{x}} \:+{e}^{−{x}} \right)}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\:\Rightarrow \\ $$$${I}={Re}\left(\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{i}\left({e}^{{x}} +{e}^{−{x}} \right)} }{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\right) \\ $$$${let}\:\varphi\left({z}\right)=\frac{{e}^{{i}\left({e}^{{z}} +{e}^{−{z}} \right)} }{\left({z}^{\mathrm{2}} \:+{z}+\mathrm{1}\right)^{\mathrm{2}} }\:{poles}\:{of}\:\varphi? \\ $$$${z}^{\mathrm{2}} +{z}+\mathrm{1}=\mathrm{0}\:\rightarrow\Delta=−\mathrm{3}\:\Rightarrow \\ $$$${z}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:{and}\:{z}_{\mathrm{2}} =\frac{−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$={e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \:\Rightarrow\varphi\left({z}\right)=\frac{{e}^{{i}\left({e}^{{z}} +{e}^{−{z}} \right)} }{\left({z}−{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} \left({z}−{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} } \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:= \\ $$$$\mathrm{2}{i}\pi\left\{\:{Re}\left(\varphi,{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)+{Res}\left(\varphi,{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\right\} \\ $$$${Res}\left(\varphi,{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)={lim}_{{z}\rightarrow{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} } \frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left({z}−{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right)\varphi\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 10/Jan/20
forgive ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,e^((i2π)/3) ) and Res(ϕ,e^(i((2π)/3)) )=lim_(z→e^((i2π)/3) ) (1/((2−1)!)){(z−e^((i2π)/3) )ϕ(z)}^((1)) =lim_(z→e^((i2π)/3) ) {(e^(i( e^z +e^(−z) )) /((z−e^(−((i2π)/3)) )^2 ))} =lim_(z→e^((i2π)/3) ) { ((i(e^z −e^(−z) )e^(i(e^z +e^(−z) )) (z−e^(−((i2π)/3)) )^2 −2(z−e^(−((i2π)/3)) )e^(i(e^x +e^(−x) )) )/((z−e^(−((i2π)/3)) )^4 ))} =lim_(z→e^((i2π)/3) ) {{ i(e^z −e^(−z) )(z−e^(−((i2π)/3)) )−2}e^(i(e^z −e^(−z) )) ×(z−e^(−((i2π)/3)) )^(−3) =(({−2sin(((2π)/3))2 sh( e^((i2π)/3) )−2}e^(2ish(e^((i2π)/3) )) )/((2i sin(((2π)/3)))^3 )) =((−2{2sin(((2π)/3))sh(e^((i2π)/3) )+1} e^(2ish(e^((i2π)/3) )) )/(−8i(((√3)/2))^3 )) =((((√3)sh(e^((i2π)/3) )+1)e^(2ish(e^(((i2π)/3) ) )) )/(4i ×(3(√3)))) =(((1+(√3)sh(−(1/2)+i((√3)/2)))e^(2i sh(−(1/2)+((i(√3))/2))) )/(12i(√3))) ⇒∫_(−∞) ^(+∞) ϕ(z)dz =(π/(6(√3)))(1+(√3)×((e^(−(1/2)+i((√3)/2)) −e^(−(−(1/2)+((i(√3))/2))) )/2)) e^(2i(((e^(−(1/2)+((i(√3))/2)) −e^(−(−(1/2)+((i(√3))/2))) )/2)) =(π/(6(√3)))( 1+((√3)/2)( e^(−(1/2)) (cos(((√3)/2))+isin(((√3)/2))−e^(1/2) (cos(((√3)/2))−isin(((√3)/2))) ×e^(i( e^(−(1/2)) (cos(((√3)/2))+isin(((√3)/2))−e^(1/2) (cos(((√3)/2))−isin(((√3)/2)))) rest to extract Re(of this quantity)...be continued...
$${forgive}\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\:\:{and} \\ $$$${Res}\left(\varphi,{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right)={lim}_{{z}\rightarrow{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} } \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left({z}−{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\varphi\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} } \:\:\:\:\left\{\frac{{e}^{{i}\left(\:{e}^{{z}} \:+{e}^{−{z}} \right)} }{\left({z}−{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} }\right\} \\ $$$$={lim}_{{z}\rightarrow{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} } \:\:\:\left\{\:\:\frac{{i}\left({e}^{{z}} −{e}^{−{z}} \right){e}^{{i}\left({e}^{{z}} +{e}^{−{z}} \right)} \left({z}−{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} −\mathrm{2}\left({z}−{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right){e}^{{i}\left({e}^{{x}} +{e}^{−{x}} \right)} }{\left({z}−{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)^{\mathrm{4}} }\right\} \\ $$$$={lim}_{{z}\rightarrow{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} } \:\:\:\left\{\left\{\:{i}\left({e}^{{z}} −{e}^{−{z}} \right)\left({z}−{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)−\mathrm{2}\right\}{e}^{{i}\left({e}^{{z}} −{e}^{−{z}} \right)} ×\left({z}−{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)^{−\mathrm{3}} \right. \\ $$$$=\frac{\left\{−\mathrm{2}{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\mathrm{2}\:{sh}\left(\:{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)−\mathrm{2}\right\}{e}^{\mathrm{2}{ish}\left({e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)} }{\left(\mathrm{2}{i}\:{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)^{\mathrm{3}} } \\ $$$$=\frac{−\mathrm{2}\left\{\mathrm{2}{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right){sh}\left({e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)+\mathrm{1}\right\}\:{e}^{\mathrm{2}{ish}\left({e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)} }{−\mathrm{8}{i}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{3}} }\:=\frac{\left(\sqrt{\mathrm{3}}{sh}\left({e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)+\mathrm{1}\right){e}^{\mathrm{2}{ish}\left({e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}\:} \right)} }{\mathrm{4}{i}\:×\left(\mathrm{3}\sqrt{\mathrm{3}}\right)} \\ $$$$=\frac{\left(\mathrm{1}+\sqrt{\mathrm{3}}{sh}\left(−\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\right){e}^{\mathrm{2}{i}\:{sh}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} }{\mathrm{12}{i}\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\frac{\pi}{\mathrm{6}\sqrt{\mathrm{3}}}\left(\mathrm{1}+\sqrt{\mathrm{3}}×\frac{{e}^{−\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} −{e}^{−\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} }{\mathrm{2}}\right)\:{e}^{\mathrm{2}{i}\left(\frac{{e}^{−\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}} −{e}^{−\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} }{\mathrm{2}}\right.} \\ $$$$=\frac{\pi}{\mathrm{6}\sqrt{\mathrm{3}}}\left(\:\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left({cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+{isin}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)−{e}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)−{isin}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\right)\right.\right.\right. \\ $$$$×{e}^{{i}\left(\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left({cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+{isin}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)−{e}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)−{isin}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\right)\right.\right.} \\ $$$${rest}\:{to}\:{extract}\:{Re}\left({of}\:{this}\:{quantity}\right)…{be}\:{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *