Question Number 138128 by mathmax by abdo last updated on 10/Apr/21
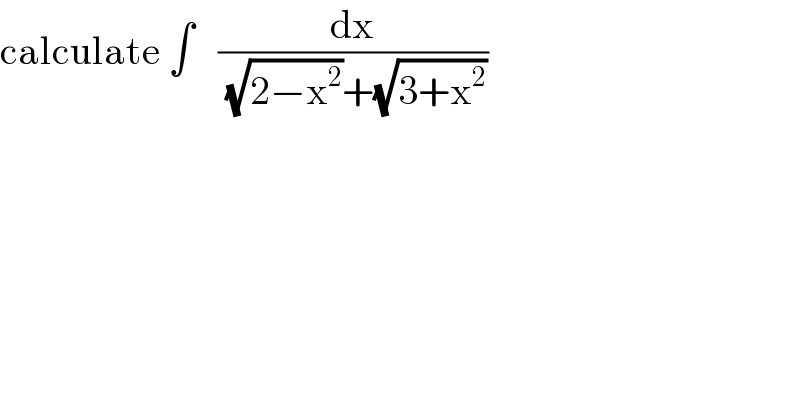
$$\mathrm{calculate}\:\int\:\:\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }+\sqrt{\mathrm{3}+\mathrm{x}^{\mathrm{2}} }} \\ $$
Answered by MJS_new last updated on 10/Apr/21
![∫(dx/( (√(2−x^2 ))+(√(3+x^2 ))))=∫((√(x^2 +3))/(2x^2 +1))dx−∫((√(2−x^2 ))/(2x^2 +1))dx ∫((√(x^2 +3))/(2x^2 +1))dx= [u=((x+(√(x^2 +3)))/( (√3))) → dx=((√(3(x^2 +3)))/(x+(√(x^2 +3))))du] =(3/2)∫(((u^2 +1)^2 )/(u(3u^4 −4u^2 +3)))du= =(1/2)∫(du/u)+((√(30))/(12))∫(du/(u^2 −((√(30))/3)u+3))−((√(30))/(12))∫(du/(u^2 +((√(30))/3)u+3))= =(1/2)ln u +((√5)/2)arctan ((√6)u−(√5)) −((√5)/2)arctan ((√6)u+(√5)) = =(1/2)ln (x+(√(x^2 +3))) +((√5)/2)(arctan ((√2)x−(√5)+(√(2(x^2 +3)))) −arctan ((√2)x+(√5)+(√(2(x^2 +3))))) [1] ∫((√(2−x^2 ))/(2x^2 +1))dx= [v=(x/( (√(2−x^2 )))) → dx=(((2−x^2 )^(3/2) )/2)dv] =2∫(dv/((v^2 +1)(5v^2 +1)))=(1/2)∫(dv/(v^2 +(1/5)))−(1/2)∫(dv/(v^2 +1))= =((√5)/2)arctan (√5)v −(1/2)arctan v = =((√5)/2)arctan (((√5)x)/( (√(2−x^2 )))) −(1/2)arctan (x/( (√(2−x^2 )))) [2] answer is [1]+[2]+C](https://www.tinkutara.com/question/Q138178.png)
$$\int\frac{{dx}}{\:\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }+\sqrt{\mathrm{3}+{x}^{\mathrm{2}} }}=\int\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{dx}−\int\frac{\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\int\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}{\:\sqrt{\mathrm{3}}}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{3}\left({x}^{\mathrm{2}} +\mathrm{3}\right)}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}{du}\right] \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{{u}\left(\mathrm{3}{u}^{\mathrm{4}} −\mathrm{4}{u}^{\mathrm{2}} +\mathrm{3}\right)}{du}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{du}}{{u}}+\frac{\sqrt{\mathrm{30}}}{\mathrm{12}}\int\frac{{du}}{{u}^{\mathrm{2}} −\frac{\sqrt{\mathrm{30}}}{\mathrm{3}}{u}+\mathrm{3}}−\frac{\sqrt{\mathrm{30}}}{\mathrm{12}}\int\frac{{du}}{{u}^{\mathrm{2}} +\frac{\sqrt{\mathrm{30}}}{\mathrm{3}}{u}+\mathrm{3}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{u}\:+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{arctan}\:\left(\sqrt{\mathrm{6}}{u}−\sqrt{\mathrm{5}}\right)\:−\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{arctan}\:\left(\sqrt{\mathrm{6}}{u}+\sqrt{\mathrm{5}}\right)\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)\:+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\left(\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{x}−\sqrt{\mathrm{5}}+\sqrt{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{3}\right)}\right)\:−\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{x}+\sqrt{\mathrm{5}}+\sqrt{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{3}\right)}\right)\right)\:\:\:\:\:\left[\mathrm{1}\right] \\ $$$$\int\frac{\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\left[{v}=\frac{{x}}{\:\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}\:\rightarrow\:{dx}=\frac{\left(\mathrm{2}−{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }{\mathrm{2}}{dv}\right] \\ $$$$=\mathrm{2}\int\frac{{dv}}{\left({v}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{5}{v}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dv}}{{v}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{5}}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dv}}{{v}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{arctan}\:\sqrt{\mathrm{5}}{v}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:{v}\:= \\ $$$$=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{5}}{x}}{\:\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:\frac{{x}}{\:\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}\:\:\:\:\:\left[\mathrm{2}\right] \\ $$$$\mathrm{answer}\:\mathrm{is}\:\left[\mathrm{1}\right]+\left[\mathrm{2}\right]+{C} \\ $$
Commented by mathmax by abdo last updated on 10/Apr/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{mjs} \\ $$
