calculate-e-3x-2-2x-dx-

Question Number 73491 by abdomathmax last updated on 13/Nov/19

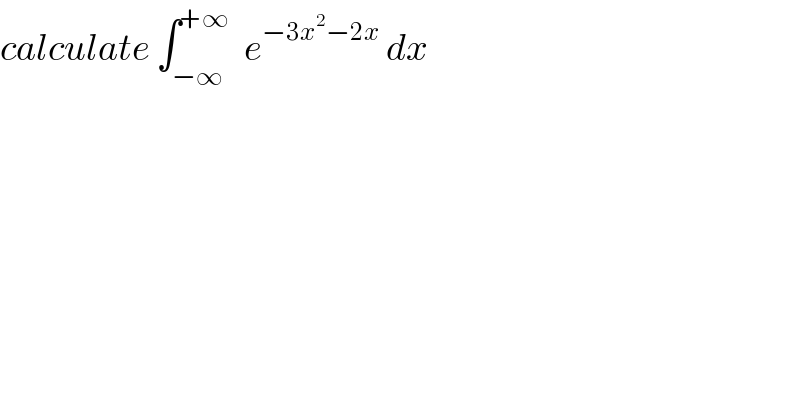
c a l c u l a t e \int_{- \infty}^{+ \infty} e^{- 3 x^{2} - 2 x} d x

Commented by mathmax by abdo last updated on 14/Nov/19

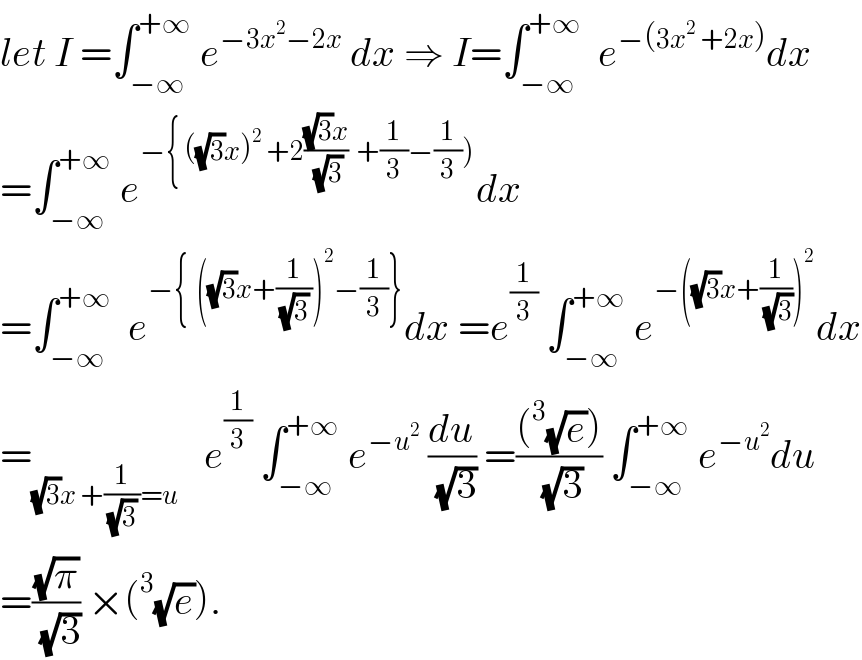
l e t I = \int_{- \infty}^{+ \infty} e^{- 3 x^{2} - 2 x} d x \Rightarrow I = \int_{- \infty}^{+ \infty} e^{- (3 x^{2} + 2 x)} d x

= \int_{- \infty}^{+ \infty} e^{- {{(\sqrt{3} x)}^{2} + 2 \frac{\sqrt{3} x}{\sqrt{3}} + \frac{1}{3} - \frac{1}{3})} d x

= \int_{- \infty}^{+ \infty} e^{- {{(\sqrt{3} x + \frac{1}{\sqrt{3}})}^{2} - \frac{1}{3}}} d x = e^{\frac{1}{3}} \int_{- \infty}^{+ \infty} e^{- {(\sqrt{3} x + \frac{1}{\sqrt{3}})}^{2}} d x

=_{\sqrt{3} x + \frac{1}{\sqrt{3}} = u} e^{\frac{1}{3}} \int_{- \infty}^{+ \infty} e^{- u^{2}} \frac{d u}{\sqrt{3}} = \frac{(^{3} \sqrt{e})}{\sqrt{3}} \int_{- \infty}^{+ \infty} e^{- u^{2}} d u

= \frac{\sqrt{π}}{\sqrt{3}} \times (^{3} \sqrt{e}) .