Question Number 74223 by mathmax by abdo last updated on 20/Nov/19
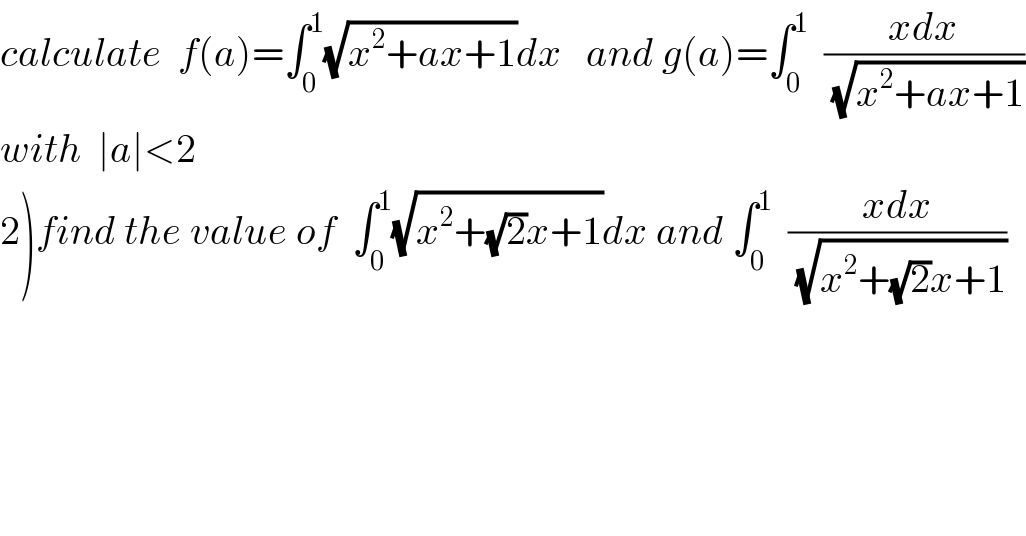
$${calculate}\:\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}^{\mathrm{2}} +{ax}+\mathrm{1}}{dx}\:\:\:{and}\:{g}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{xdx}}{\:\sqrt{{x}^{\mathrm{2}} +{ax}+\mathrm{1}}} \\ $$$${with}\:\:\mid{a}\mid<\mathrm{2} \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}^{\mathrm{2}} +\sqrt{\mathrm{2}}{x}+\mathrm{1}}{dx}\:{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{xdx}}{\:\sqrt{{x}^{\mathrm{2}} +\sqrt{\mathrm{2}}{x}+\mathrm{1}}} \\ $$
Answered by mind is power last updated on 20/Nov/19
![f(a)=∫_0 ^1 (√((x+(a/2))^2 +((4−a^2 )/4)))dx let (x+(a/2))=(√((4−a^2 )/4)) sh(u) ⇒dx=(√((4−a^2 )/4)).ch(u)du ∫_(argsh((a/( (√(4−a^2 )))))) ^(argsh((√((a+2)/(2−a))))) .((4−a^2 )/4).ch^2 (u)du =∫((4−a^2 )/4).(((ch(2u)+1)/2))du =((4−a^2 )/4)[((sh(2u))/4)+(u/2)]_(argsh((a/( (√(4−a^2 )))))) ^(argsh((√((a+2)/(2−a))))) sh(2u)=2sh(u)ch(u) sh(2argsh(t))=2t.(√(1+t^2 )) =((4−a^2 )/4) [(((√((a+2)/(2−a)))(√(4/(2−a)))−(a/( (√(4−a^2 ))))(√((4−a^2 +a)/(4−a^2 ))))/2)+ (1/2)argsh((√((a+2)/(2−a))))−(1/2)argsh((a/( (√(4−a^2 )))))=f(a) g(a)=2f′(a) 2)=f((√2)),g((√2))](https://www.tinkutara.com/question/Q74245.png)
$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\left({x}+\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{4}−{a}^{\mathrm{2}} }{\mathrm{4}}}{dx} \\ $$$${let}\:\left({x}+\frac{{a}}{\mathrm{2}}\right)=\sqrt{\frac{\mathrm{4}−{a}^{\mathrm{2}} }{\mathrm{4}}}\:{sh}\left({u}\right) \\ $$$$\Rightarrow{dx}=\sqrt{\frac{\mathrm{4}−{a}^{\mathrm{2}} }{\mathrm{4}}}.{ch}\left({u}\right){du} \\ $$$$\int_{{argsh}\left(\frac{{a}}{\:\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}\right)} ^{{argsh}\left(\sqrt{\frac{{a}+\mathrm{2}}{\mathrm{2}−{a}}}\right)} .\frac{\mathrm{4}−{a}^{\mathrm{2}} }{\mathrm{4}}.{ch}^{\mathrm{2}} \left({u}\right){du} \\ $$$$=\int\frac{\mathrm{4}−{a}^{\mathrm{2}} }{\mathrm{4}}.\left(\frac{{ch}\left(\mathrm{2}{u}\right)+\mathrm{1}}{\mathrm{2}}\right){du} \\ $$$$=\frac{\mathrm{4}−{a}^{\mathrm{2}} }{\mathrm{4}}\left[\frac{{sh}\left(\mathrm{2}{u}\right)}{\mathrm{4}}+\frac{{u}}{\mathrm{2}}\right]_{{argsh}\left(\frac{{a}}{\:\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}\right)} ^{{argsh}\left(\sqrt{\frac{{a}+\mathrm{2}}{\mathrm{2}−{a}}}\right)} \\ $$$${sh}\left(\mathrm{2}{u}\right)=\mathrm{2}{sh}\left({u}\right){ch}\left({u}\right) \\ $$$${sh}\left(\mathrm{2}{argsh}\left({t}\right)\right)=\mathrm{2}{t}.\sqrt{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{4}−{a}^{\mathrm{2}} }{\mathrm{4}}\:\:\left[\frac{\sqrt{\frac{{a}+\mathrm{2}}{\mathrm{2}−{a}}}\sqrt{\frac{\mathrm{4}}{\mathrm{2}−{a}}}−\frac{{a}}{\:\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}\sqrt{\frac{\mathrm{4}−{a}^{\mathrm{2}} +{a}}{\mathrm{4}−{a}^{\mathrm{2}} }}}{\mathrm{2}}+\:\:\frac{\mathrm{1}}{\mathrm{2}}{argsh}\left(\sqrt{\frac{{a}+\mathrm{2}}{\mathrm{2}−{a}}}\right)−\frac{\mathrm{1}}{\mathrm{2}}{argsh}\left(\frac{{a}}{\:\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}\right)={f}\left({a}\right)\right. \\ $$$${g}\left({a}\right)=\mathrm{2}{f}'\left({a}\right) \\ $$$$\left.\mathrm{2}\right)={f}\left(\sqrt{\mathrm{2}}\right),{g}\left(\sqrt{\mathrm{2}}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 20/Nov/19

$${thank}\:{you}\:{sir}. \\ $$
