Question Number 74888 by abdomathmax last updated on 03/Dec/19
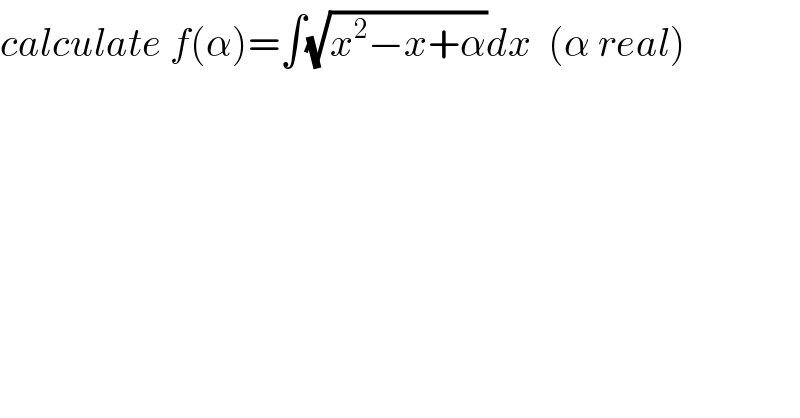
$${calculate}\:{f}\left(\alpha\right)=\int\sqrt{{x}^{\mathrm{2}} −{x}+\alpha}{dx}\:\:\left(\alpha\:{real}\right) \\ $$
Commented by MJS last updated on 03/Dec/19

$$\mathrm{no}\:\mathrm{borders}? \\ $$
Commented by mathmax by abdo last updated on 03/Dec/19

$${yes} \\ $$
Commented by mathmax by abdo last updated on 03/Dec/19

$${f}\left(\alpha\right)=\int\sqrt{{x}^{\mathrm{2}} −{x}+\alpha}{dx} \\ $$$${let}\:{solve}\:{x}^{\mathrm{2}} −{x}+\alpha\:=\mathrm{0}\:\rightarrow\Delta=\mathrm{1}−\mathrm{4}\alpha \\ $$$${case}\left(\mathrm{1}\right)\:\mathrm{1}−\mathrm{4}\alpha<\mathrm{0}\:\Rightarrow{x}^{\mathrm{2}} −{x}+\alpha\:={x}^{\mathrm{2}} −\mathrm{2}\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\:+\alpha−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$=\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{4}\alpha−\mathrm{1}}{\mathrm{4}}\:\:\:\:\left(\:\mathrm{4}\alpha−\mathrm{1}>\mathrm{0}\right)\:\Rightarrow \\ $$$${f}\left(\alpha\right)\:=_{{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{4}\alpha−\mathrm{1}}}{\mathrm{2}}{sh}\left({u}\right)} \:\:\:\int\:\:\sqrt{\frac{\mathrm{4}\alpha−\mathrm{1}}{\mathrm{4}}}{ch}\left({u}\right)\frac{\sqrt{\mathrm{4}\alpha−\mathrm{1}}}{\mathrm{2}}{ch}\left({u}\right){du} \\ $$$$=\frac{\mathrm{4}\alpha−\mathrm{1}}{\mathrm{4}}\:\int\:{ch}^{\mathrm{2}} \left({u}\right){du}\:=\frac{\mathrm{4}\alpha−\mathrm{1}}{\mathrm{4}}\:\int\frac{\mathrm{1}+{ch}\left(\mathrm{2}{u}\right)}{\mathrm{2}}{du} \\ $$$$=\frac{\left(\mathrm{4}\alpha−\mathrm{1}\right)}{\mathrm{8}}\:{u}\:\:+\frac{\mathrm{4}\alpha−\mathrm{1}}{\mathrm{16}}{sh}\left(\mathrm{2}{u}\right)\:+{C} \\ $$$$=\frac{\left(\mathrm{4}\alpha−\mathrm{1}\right)}{\mathrm{8}}\:{argsh}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{4}\alpha−\mathrm{1}}}\right)\:+\frac{\mathrm{4}\alpha−\mathrm{1}}{\mathrm{8}}\:{sh}\left({u}\right){ch}\left({u}\right)\:+{c} \\ $$$$=\frac{\left(\mathrm{4}\alpha−\mathrm{1}\right)}{\mathrm{8}}{ln}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{4}\alpha−\mathrm{1}}}\:+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{4}\alpha−\mathrm{1}}\:}\right)^{\mathrm{2}} }\right)\:+\frac{\mathrm{4}\alpha−\mathrm{1}}{\mathrm{8}}×\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{4}\alpha−\mathrm{1}}}\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{4}\alpha−\mathrm{1}}}\right)^{\mathrm{2}} }+{C} \\ $$$${case}\:\left(\mathrm{2}\right)\:\:\:\mathrm{1}−\mathrm{4}\alpha>\mathrm{0}\:\Rightarrow{x}_{\mathrm{1}} =\frac{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{4}\alpha}}{\mathrm{2}}\:\:{and}\:\:{x}_{\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{4}\alpha}}{\mathrm{2}} \\ $$$${f}\left(\alpha\right)=\int\sqrt{\left({x}−{x}_{\mathrm{1}} \right)\left({x}−{x}_{\mathrm{2}} \right)}{dx}\:\:{changement}\:\:\sqrt{{x}−{x}_{\mathrm{1}} }={u}\:{givex}−{x}_{\mathrm{1}} ={u}^{\mathrm{2}} \\ $$$${f}\left(\alpha\right)\:=\int\:{u}\sqrt{{u}^{\mathrm{2}} \:+{x}_{\mathrm{1}} −{x}_{\mathrm{2}} }\left(\mathrm{2}{u}\right){du} \\ $$$$=\mathrm{2}\:\int\:{u}^{\mathrm{2}} \sqrt{{u}^{\mathrm{2}} +\sqrt{\mathrm{1}−\mathrm{4}\alpha}}\:{du}\:\:{we}\:{do}\:{the}\:{changement}\:{u}=\left(^{\mathrm{4}} \sqrt{\mathrm{1}−\mathrm{4}\alpha}\right){sh}\left({z}\right) \\ $$$$\Rightarrow{f}\left(\alpha\right)=\mathrm{2}\:\int\:\:\sqrt{\mathrm{1}−\mathrm{4}\alpha}\sqrt{\mathrm{1}−\mathrm{4}\alpha}{sh}^{\mathrm{2}} \left({z}\right){ch}\left({z}\right)\left(^{\mathrm{4}} \sqrt{\mathrm{1}−\mathrm{4}\alpha}\right){ch}\left({z}\right){dz} \\ $$$$=\mathrm{2}\left(\mathrm{1}−\mathrm{4}\alpha\right)\left(^{\mathrm{4}} \sqrt{\mathrm{1}−\mathrm{4}\alpha}\right)\:\int\:{sh}^{\mathrm{2}} \left({z}\right){ch}^{\mathrm{2}} \left({z}\right){dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{4}\alpha\right)^{\frac{\mathrm{5}}{\mathrm{4}}} \:\:\int\:\:{sh}^{\mathrm{2}} \left(\mathrm{2}{z}\right){dz}\:=….{be}\:{continued}… \\ $$$$ \\ $$
Answered by MJS last updated on 03/Dec/19
![∫(√(x^2 −x+α))dx=∫(√((x−(1/2))^2 +α−(1/4)))dx= [t=((2x−1)/( (√(4α−1)))) → dx=((√(4α−1))/2)dt] =((4α−1)/4)∫(√(t^2 +1))dt= =((4α−1)/8)(t(√(t^2 +1))+ln (t+(√(t^2 +1)))= ... =(((2x−1)(√(x^2 −x+α)))/4)+((4α−1)/8)ln (2x−1+2(√(x^2 −x+α))) +C](https://www.tinkutara.com/question/Q74906.png)
$$\int\sqrt{{x}^{\mathrm{2}} −{x}+\alpha}{dx}=\int\sqrt{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\alpha−\frac{\mathrm{1}}{\mathrm{4}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{4}\alpha−\mathrm{1}}}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{4}\alpha−\mathrm{1}}}{\mathrm{2}}{dt}\right] \\ $$$$=\frac{\mathrm{4}\alpha−\mathrm{1}}{\mathrm{4}}\int\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}{dt}= \\ $$$$=\frac{\mathrm{4}\alpha−\mathrm{1}}{\mathrm{8}}\left({t}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}+\mathrm{ln}\:\left({t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\right)=\right. \\ $$$$… \\ $$$$=\frac{\left(\mathrm{2}{x}−\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\alpha}}{\mathrm{4}}+\frac{\mathrm{4}\alpha−\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:\left(\mathrm{2}{x}−\mathrm{1}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} −{x}+\alpha}\right)\:+{C} \\ $$
