Question Number 133964 by mathocean1 last updated on 26/Feb/21
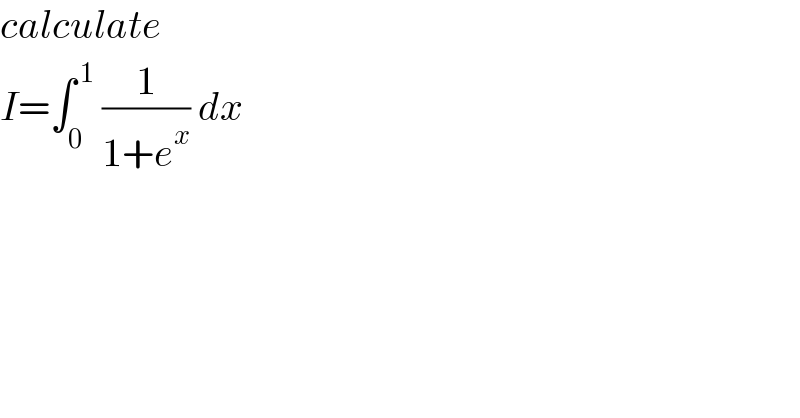
$${calculate}\: \\ $$$${I}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{1}+{e}^{{x}} }\:{dx} \\ $$
Answered by bobhans last updated on 26/Feb/21
![∫ ((e^x +1−e^x )/(1+e^x )) dx = x−∫ (e^x /(1+e^x )) dx = x−ln (1+e^x )+c I= [ x−ln (1+e^x ) ]_0 ^1 = 1−ln (1+e)+ln (2) = 1+ln ((2/(1+e))) = ln (((2e)/(1+e)))](https://www.tinkutara.com/question/Q133965.png)
$$\int\:\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{1}−\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\:\mathrm{dx}\:=\:\mathrm{x}−\int\:\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\:\mathrm{dx} \\ $$$$=\:\mathrm{x}−\mathrm{ln}\:\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)+\mathrm{c} \\ $$$$ \\ $$$$\mathcal{I}=\:\left[\:\mathrm{x}−\mathrm{ln}\:\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)\:\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:\mathrm{1}−\mathrm{ln}\:\left(\mathrm{1}+\mathrm{e}\right)+\mathrm{ln}\:\left(\mathrm{2}\right) \\ $$$$=\:\mathrm{1}+\mathrm{ln}\:\left(\frac{\mathrm{2}}{\mathrm{1}+\mathrm{e}}\right)\:=\:\mathrm{ln}\:\left(\frac{\mathrm{2e}}{\mathrm{1}+\mathrm{e}}\right) \\ $$
Answered by Olaf last updated on 26/Feb/21
![I = ∫_0 ^1 (dx/(1+e^x )) I = ∫_0 ^1 (((1+e^x )/(1+e^x ))−(e^x /(1+e^x )))dx I = [x−ln(1+e^x )]_0 ^1 I = 1−ln(1+e)+ln2 I = 1+ln((2/(1+e)))](https://www.tinkutara.com/question/Q133966.png)
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+{e}^{{x}} } \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}+{e}^{{x}} }{\mathrm{1}+{e}^{{x}} }−\frac{{e}^{{x}} }{\mathrm{1}+{e}^{{x}} }\right){dx} \\ $$$$\mathrm{I}\:=\:\left[{x}−\mathrm{ln}\left(\mathrm{1}+{e}^{{x}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{I}\:=\:\mathrm{1}−\mathrm{ln}\left(\mathrm{1}+{e}\right)+\mathrm{ln2} \\ $$$$\mathrm{I}\:=\:\mathrm{1}+\mathrm{ln}\left(\frac{\mathrm{2}}{\mathrm{1}+{e}}\right) \\ $$
Answered by mathmax by abdo last updated on 26/Feb/21
![I =∫_0 ^1 (dx/(e^x +1)) changement e^x =t give x=lnt ⇒ I =∫_1 ^e (dt/(t(t+1))) =∫_1 ^e ((1/t)−(1/(t+1)))dt =[ln∣(t/(t+1))∣]_1 ^e =ln((e/(e+1)))−ln((1/2)) =1−ln(e+1)+ln(2)](https://www.tinkutara.com/question/Q133986.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{e}^{\mathrm{x}} \:+\mathrm{1}}\:\mathrm{changement}\:\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}\:\mathrm{give}\:\mathrm{x}=\mathrm{lnt}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{1}} ^{\mathrm{e}} \:\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{t}+\mathrm{1}\right)}\:=\int_{\mathrm{1}} ^{\mathrm{e}} \:\left(\frac{\mathrm{1}}{\mathrm{t}}−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\right)\mathrm{dt}\:=\left[\mathrm{ln}\mid\frac{\mathrm{t}}{\mathrm{t}+\mathrm{1}}\mid\right]_{\mathrm{1}} ^{\mathrm{e}} \:=\mathrm{ln}\left(\frac{\mathrm{e}}{\mathrm{e}+\mathrm{1}}\right)−\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\mathrm{1}−\mathrm{ln}\left(\mathrm{e}+\mathrm{1}\right)+\mathrm{ln}\left(\mathrm{2}\right) \\ $$
