Question Number 66483 by ~ À ® @ 237 ~ last updated on 16/Aug/19

$$\:{calculate}\:\:\:\:\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\:\zeta\left({k}\right)\:\:\:\:\:\:\:{if}\:\:\:\:\zeta\left({s}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\:\frac{\mathrm{1}}{{n}^{{s}} }\: \\ $$
Commented by mathmax by abdo last updated on 16/Aug/19

$${let}\:{S}\:=\sum_{{k}=\mathrm{2}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\xi\left({k}\right)\:\Rightarrow\:{S}\:=\sum_{{k}=\mathrm{2}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{{k}} }\right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(\sum_{{k}=\mathrm{2}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}\:{n}^{{k}} }\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \left(\sum_{{k}=\mathrm{2}} ^{\infty} \frac{\mathrm{1}}{{k}}\left(−\frac{\mathrm{1}}{{n}}\right)^{{k}} \right) \\ $$$${let}\:{find}\:{f}\left({x}\right)\:=\sum_{{k}=\mathrm{2}} ^{\infty} \frac{{x}^{{k}} }{{k}}\:{with}\:\mid{x}\mid<\mathrm{1}\Rightarrow{f}^{'} \left({x}\right)=\sum_{{k}=\mathrm{2}} ^{\infty} {x}^{{k}−\mathrm{1}} \:=\sum_{{k}=\mathrm{1}} ^{\infty} {x}^{{k}} \\ $$$$={x}\:\sum_{{k}=\mathrm{1}} ^{\infty} \:{x}^{{k}−\mathrm{1}} \left[={x}\:\sum_{{k}=\mathrm{0}} ^{\infty} \:{x}^{{k}} \:=\frac{{x}}{\mathrm{1}−{x}}\:\Rightarrow{f}\left({x}\right)\:=\int\frac{{x}}{\mathrm{1}−{x}}{dx}\:+{c}\right. \\ $$$$=−\int\frac{{x}}{{x}−\mathrm{1}}{dx}+{c}\:=−\int\frac{{x}−\mathrm{1}+\mathrm{1}}{{x}−\mathrm{1}}{dx}\:+{c}\:=−{x}+{ln}\mid{x}−\mathrm{1}\mid\:+{c} \\ $$$${f}\left(\mathrm{0}\right)\:=\mathrm{0}={c}\:\Rightarrow{f}\left({x}\right)\:=−{x}+{ln}\mid{x}−\mathrm{1}\mid\Rightarrow \\ $$$$\sum_{{k}=\mathrm{2}} ^{\infty} \frac{\mathrm{1}}{{k}}\left(−\frac{\mathrm{1}}{{n}}\right)^{{k}} \:=\frac{\mathrm{1}}{{n}}+{ln}\mid\frac{\mathrm{1}}{{n}}+\mathrm{1}\mid\:=\frac{\mathrm{1}}{{n}}\:+{ln}\left(\frac{{n}+\mathrm{1}}{{n}}\right) \\ $$$$=\frac{\mathrm{1}}{{n}}+{ln}\left({n}\right)−{ln}\left({n}+\mathrm{1}\right)\:\Rightarrow \\ $$$${S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(\frac{\mathrm{1}}{{n}}\:+{ln}\left({n}\right)−{ln}\left({n}+\mathrm{1}\right)\right)={lim}_{{n}\rightarrow+\infty} \:\:{S}_{{n}} \:{with} \\ $$$${S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \left(\frac{\mathrm{1}}{{k}}+{ln}\left({k}\right)−{ln}\left({k}+\mathrm{1}\right)\right)\:=\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\mathrm{1}}{{k}}\:+\sum_{{k}=\mathrm{1}} ^{{n}} \left({ln}\left({k}\right)−{ln}\left({k}+\mathrm{1}\right)\right) \\ $$$$={H}_{{n}} −{ln}\left({n}+\mathrm{1}\right)\:={H}_{{n}} −{ln}\left({n}\right)−{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\rightarrow\gamma\:\left({n}\rightarrow+\infty\right)\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{2}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\xi\left({k}\right)\:=\gamma\:\:\:\:\:\:\:\left({constant}\:{of}\:{Euler}\right) \\ $$
Commented by mathmax by abdo last updated on 17/Aug/19
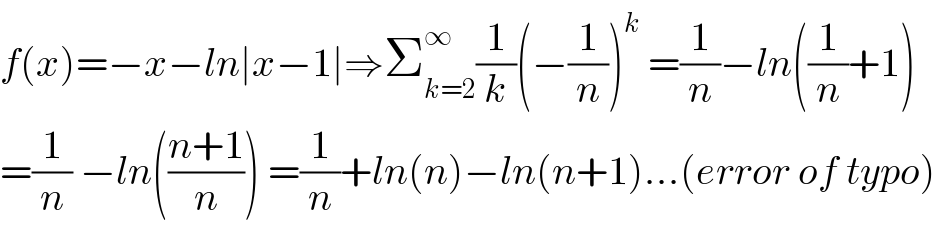
$${f}\left({x}\right)=−{x}−{ln}\mid{x}−\mathrm{1}\mid\Rightarrow\sum_{{k}=\mathrm{2}} ^{\infty} \frac{\mathrm{1}}{{k}}\left(−\frac{\mathrm{1}}{{n}}\right)^{{k}} \:=\frac{\mathrm{1}}{{n}}−{ln}\left(\frac{\mathrm{1}}{{n}}+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{{n}}\:−{ln}\left(\frac{{n}+\mathrm{1}}{{n}}\right)\:=\frac{\mathrm{1}}{{n}}+{ln}\left({n}\right)−{ln}\left({n}+\mathrm{1}\right)…\left({error}\:{of}\:{typo}\right) \\ $$
Commented by ~ À ® @ 237 ~ last updated on 17/Aug/19

$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 17/Aug/19

$${you}\:{are}\:{welcome}. \\ $$
