Question Number 134067 by bramlexs22 last updated on 27/Feb/21
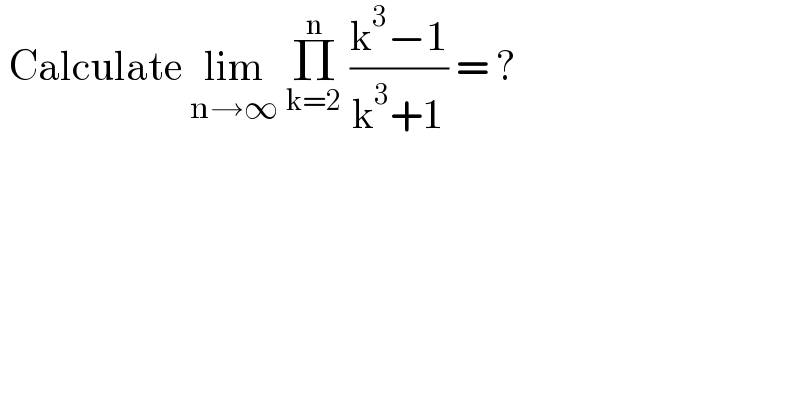
$$\:\mathrm{Calculate}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{n}} {\prod}}\:\frac{\mathrm{k}^{\mathrm{3}} −\mathrm{1}}{\mathrm{k}^{\mathrm{3}} +\mathrm{1}}\:=\:? \\ $$
Answered by john_santu last updated on 27/Feb/21
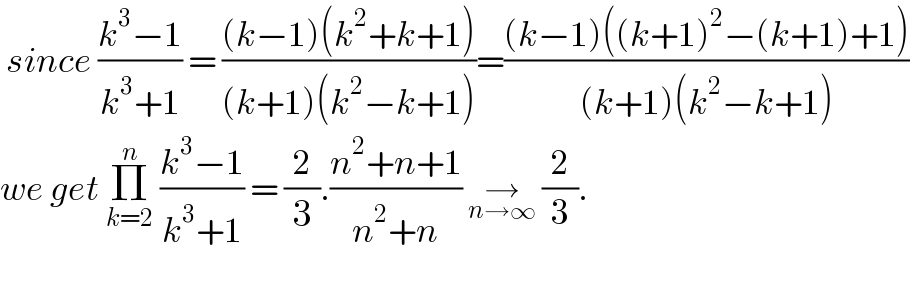
$$\:{since}\:\frac{{k}^{\mathrm{3}} −\mathrm{1}}{{k}^{\mathrm{3}} +\mathrm{1}}\:=\:\frac{\left({k}−\mathrm{1}\right)\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)}{\left({k}+\mathrm{1}\right)\left({k}^{\mathrm{2}} −{k}+\mathrm{1}\right)}=\frac{\left({k}−\mathrm{1}\right)\left(\left({k}+\mathrm{1}\right)^{\mathrm{2}} −\left({k}+\mathrm{1}\right)+\mathrm{1}\right)}{\left({k}+\mathrm{1}\right)\left({k}^{\mathrm{2}} −{k}+\mathrm{1}\right)} \\ $$$${we}\:{get}\:\underset{{k}=\mathrm{2}} {\overset{{n}} {\prod}}\:\frac{{k}^{\mathrm{3}} −\mathrm{1}}{{k}^{\mathrm{3}} +\mathrm{1}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}.\frac{{n}^{\mathrm{2}} +{n}+\mathrm{1}}{{n}^{\mathrm{2}} +{n}}\:\underset{{n}\rightarrow\infty} {\rightarrow}\:\frac{\mathrm{2}}{\mathrm{3}}. \\ $$$$ \\ $$
