Menu Close

calculate-lim-x-0-sin-x-2-xtan-x-1-cos-4x-

Tinku Tara
Pin




Question Number 65779 by mathmax by abdo last updated on 03/Aug/19
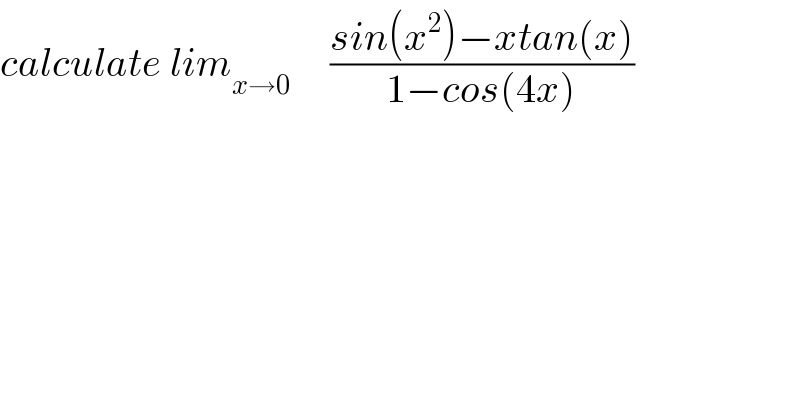
calculate lim_(x→0) ((sin(x^2 )−xtan(x))/(1−cos(4x)))
$${calculate}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\:\frac{{sin}\left({x}^{\mathrm{2}} \right)−{xtan}\left({x}\right)}{\mathrm{1}−{cos}\left(\mathrm{4}{x}\right)} \\ $$
Commented by mathmax by abdo last updated on 04/Aug/19
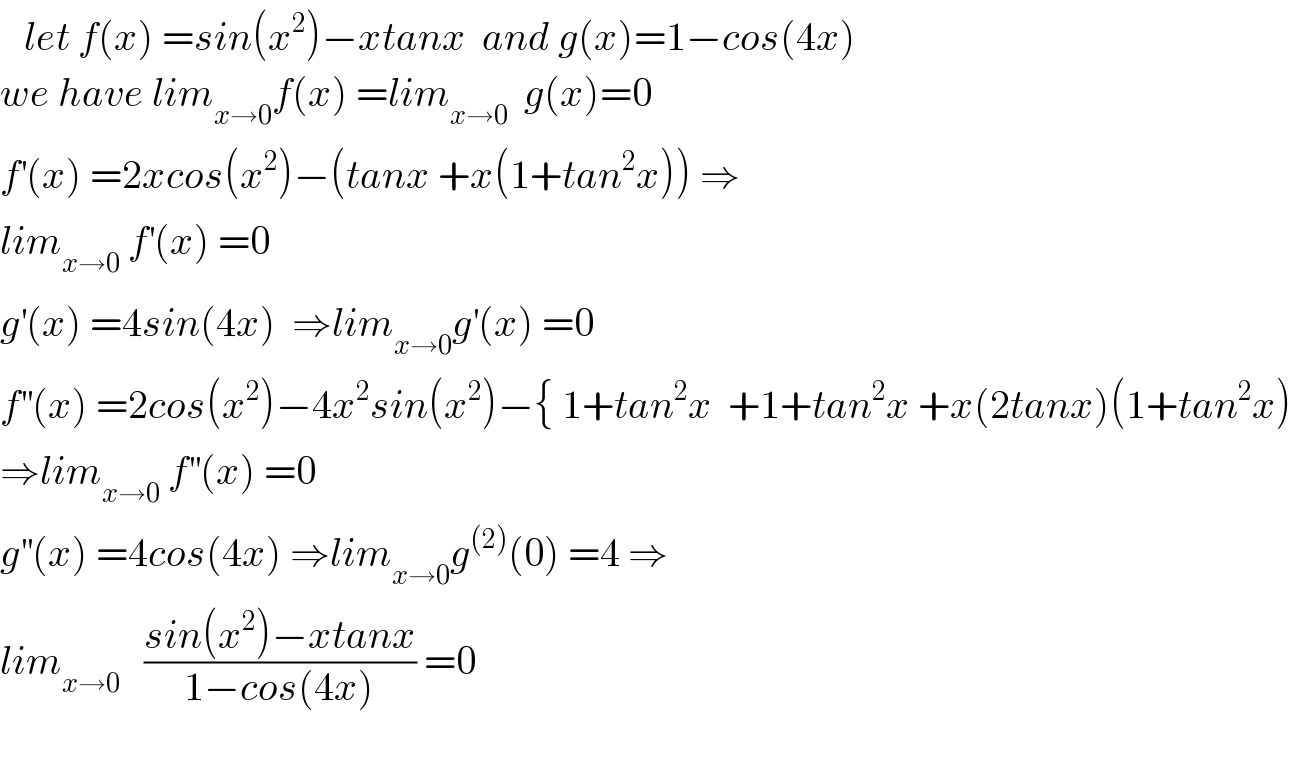
let f(x) =sin(x^2 )−xtanx and g(x)=1−cos(4x) we have lim_(x→0) f(x) =lim_(x→0) g(x)=0 f^′ (x) =2xcos(x^2 )−(tanx +x(1+tan^2 x)) ⇒ lim_(x→0) f^′ (x) =0 g^′ (x) =4sin(4x) ⇒lim_(x→0) g^′ (x) =0 f^(′′) (x) =2cos(x^2 )−4x^2 sin(x^2 )−{ 1+tan^2 x +1+tan^2 x +x(2tanx)(1+tan^2 x) ⇒lim_(x→0) f^(′′) (x) =0 g^(′′) (x) =4cos(4x) ⇒lim_(x→0) g^((2)) (0) =4 ⇒ lim_(x→0) ((sin(x^2 )−xtanx)/(1−cos(4x))) =0
$$\:\:\:{let}\:{f}\left({x}\right)\:={sin}\left({x}^{\mathrm{2}} \right)−{xtanx}\:\:{and}\:{g}\left({x}\right)=\mathrm{1}−{cos}\left(\mathrm{4}{x}\right) \\ $$$${we}\:{have}\:{lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)\:={lim}_{{x}\rightarrow\mathrm{0}} \:\:{g}\left({x}\right)=\mathrm{0} \\ $$$${f}^{'} \left({x}\right)\:=\mathrm{2}{xcos}\left({x}^{\mathrm{2}} \right)−\left({tanx}\:+{x}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:{f}^{'} \left({x}\right)\:=\mathrm{0} \\ $$$${g}^{'} \left({x}\right)\:=\mathrm{4}{sin}\left(\mathrm{4}{x}\right)\:\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} {g}^{'} \left({x}\right)\:=\mathrm{0} \\ $$$${f}^{''} \left({x}\right)\:=\mathrm{2}{cos}\left({x}^{\mathrm{2}} \right)−\mathrm{4}{x}^{\mathrm{2}} {sin}\left({x}^{\mathrm{2}} \right)−\left\{\:\mathrm{1}+{tan}^{\mathrm{2}} {x}\:\:+\mathrm{1}+{tan}^{\mathrm{2}} {x}\:+{x}\left(\mathrm{2}{tanx}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\right. \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:{f}^{''} \left({x}\right)\:=\mathrm{0} \\ $$$${g}^{''} \left({x}\right)\:=\mathrm{4}{cos}\left(\mathrm{4}{x}\right)\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} {g}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:=\mathrm{4}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{sin}\left({x}^{\mathrm{2}} \right)−{xtanx}}{\mathrm{1}−{cos}\left(\mathrm{4}{x}\right)}\:=\mathrm{0} \\ $$$$ \\ $$

Pin