Question Number 136404 by mathmax by abdo last updated on 21/Mar/21
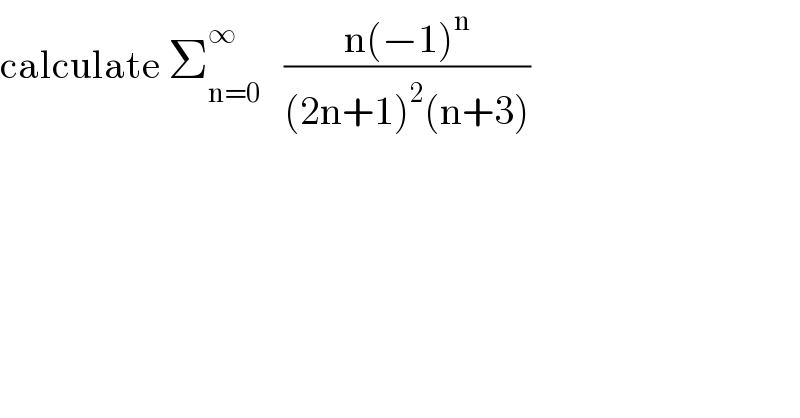
$$\mathrm{calculate}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{n}+\mathrm{3}\right)} \\ $$
Answered by mindispower last updated on 21/Mar/21

$$−\frac{\mathrm{1}}{\mathrm{2}}\left\{\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)\left({n}+\mathrm{3}\right)}−\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\right\}=−\frac{\mathrm{1}}{\mathrm{2}}{A} \\ $$$${A}=\Sigma\frac{\mathrm{2}}{\mathrm{5}}.\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{5}}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{3}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{5}}\Sigma\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{3}} }{{n}+\mathrm{3}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{5}}\underset{{n}\geqslant\mathrm{2}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}−{G} \\ $$$$=\frac{\pi}{\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{5}}\left({ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right)−{G} \\ $$$${we}\:{get}\:−\frac{\pi}{\mathrm{20}}+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{20}}+\frac{{G}}{\mathrm{2}},{G}\:{catalan}\:{constante} \\ $$$$ \\ $$
