Question Number 74884 by abdomathmax last updated on 03/Dec/19
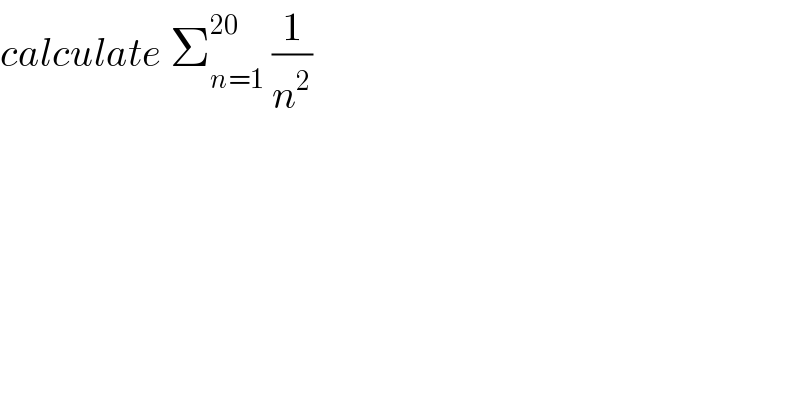
$${calculate}\:\sum_{{n}=\mathrm{1}} ^{\mathrm{20}} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 03/Dec/19
![let S=Σ_(n=1) ^(20) (1/n^2 ) ⇒ S =Σ_(p=1) ^(10) (1/((2p)^2 )) +Σ_(p=0) ^([((19)/2)]) (1/((2p+1)^2 )) =(1/4)Σ_(p=1) ^(10) (1/p^2 ) +Σ_(p=0) ^9 (1/((2p+1)^2 )) also Σ_(p=1) ^(10) (1/p^2 ) =(1/4)Σ_(p=1) ^5 (1/p^2 ) +Σ_(p=0) ^4 (1/((2p+1)^2 )) ⇒ S =(1/4){(1/4)Σ_(p=1) ^5 (1/p^2 ) +Σ_(p=0) ^4 (1/((2p+1)^2 ))}+Σ_(p=0) ^4 (1/((2p+1)^2 )) +Σ_(p=5) ^9 (1/((2p+1)^2 )) =(1/(16))Σ_(p=1) ^5 (1/p^2 ) +(5/4) Σ_(p=0) ^4 (1/((2p+1)^2 )) +Σ_(p=5) ^9 (1/((2p+1)^2 )) we have Σ_(p=5) ^9 (1/((2p+1)^2 )) =_(p−5=k) Σ_(k=0) ^4 (1/((2k+11)^2 )) ⇒ S =(1/(16))Σ_(p=1) ^5 (1/p^2 ) +(5/4)Σ_(p=0) ^4 (1/((2p+1)^2 )) +Σ_(p=0) ^4 (1/((2p+11)^2 )) =(1/(16))(1+(1/2^2 ) +(1/3^2 ) +(1/4^2 ) +(1/5^2 ))+(5/4)(1+(1/3^2 ) +(1/5^2 ) +(1/7^2 ) +(1/9^2 ) +(1/(11^2 ))) +(1/(11^2 )) +(1/(13^2 )) +(1/(15^2 )) +(1/(17^2 )) +(1/(19^2 )) S =(1/(16))(1+(1/4) +(1/9) +(1/(16)) +(1/(25)))+(5/4)(1+(1/9) +(1/(25)) +(1/(49)) +(1/(81)) +(1/(121))) +(1/(11^2 )) +(1/(13^2 )) +(1/(15^2 )) +(1/(17^2 )) +(1/(19^2 )) =....its eazy now to find S..](https://www.tinkutara.com/question/Q74927.png)
$${let}\:{S}=\sum_{{n}=\mathrm{1}} ^{\mathrm{20}} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\Rightarrow\:{S}\:=\sum_{{p}=\mathrm{1}} ^{\mathrm{10}} \frac{\mathrm{1}}{\left(\mathrm{2}{p}\right)^{\mathrm{2}} }\:+\sum_{{p}=\mathrm{0}} ^{\left[\frac{\mathrm{19}}{\mathrm{2}}\right]} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\sum_{{p}=\mathrm{1}} ^{\mathrm{10}} \:\frac{\mathrm{1}}{{p}^{\mathrm{2}} }\:+\sum_{{p}=\mathrm{0}} ^{\mathrm{9}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} }\:\:{also} \\ $$$$\sum_{{p}=\mathrm{1}} ^{\mathrm{10}} \:\frac{\mathrm{1}}{{p}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{4}}\sum_{{p}=\mathrm{1}} ^{\mathrm{5}} \:\frac{\mathrm{1}}{{p}^{\mathrm{2}} }\:+\sum_{{p}=\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${S}\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\frac{\mathrm{1}}{\mathrm{4}}\sum_{{p}=\mathrm{1}} ^{\mathrm{5}} \:\frac{\mathrm{1}}{{p}^{\mathrm{2}} }\:+\sum_{{p}=\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} }\right\}+\sum_{{p}=\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} }\:+\sum_{{p}=\mathrm{5}} ^{\mathrm{9}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\sum_{{p}=\mathrm{1}} ^{\mathrm{5}} \:\frac{\mathrm{1}}{{p}^{\mathrm{2}} }\:+\frac{\mathrm{5}}{\mathrm{4}}\:\sum_{{p}=\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} }\:+\sum_{{p}=\mathrm{5}} ^{\mathrm{9}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} }\:\:{we}\:{have} \\ $$$$\sum_{{p}=\mathrm{5}} ^{\mathrm{9}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} }\:=_{{p}−\mathrm{5}={k}} \:\:\sum_{{k}=\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{11}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${S}\:=\frac{\mathrm{1}}{\mathrm{16}}\sum_{{p}=\mathrm{1}} ^{\mathrm{5}} \:\frac{\mathrm{1}}{{p}^{\mathrm{2}} }\:+\frac{\mathrm{5}}{\mathrm{4}}\sum_{{p}=\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} }\:+\sum_{{p}=\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{11}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }\right)+\frac{\mathrm{5}}{\mathrm{4}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{9}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{2}} }\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{13}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{15}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{17}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{19}^{\mathrm{2}} } \\ $$$${S}\:=\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{9}}\:+\frac{\mathrm{1}}{\mathrm{16}}\:+\frac{\mathrm{1}}{\mathrm{25}}\right)+\frac{\mathrm{5}}{\mathrm{4}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{9}}\:+\frac{\mathrm{1}}{\mathrm{25}}\:+\frac{\mathrm{1}}{\mathrm{49}}\:+\frac{\mathrm{1}}{\mathrm{81}}\:+\frac{\mathrm{1}}{\mathrm{121}}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{13}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{15}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{17}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{19}^{\mathrm{2}} }\:=….{its}\:{eazy}\:{now}\:{to}\:{find}\:{S}.. \\ $$
Commented by mathmax by abdo last updated on 05/Dec/19
![another way let S =Σ_(n=1) ^(20) (1/n^2 ) ⇒ S = Σ_(n=1_(n=3k) ) ^(20) (1/n^2 ) +Σ_(n=1_(n=3k+1) ) ^(20) (1/n^2 ) +Σ_(n=1_(n=3k+2) ) ^(20) (1/n^2 ) =Σ_(n=1) ^([((20)/3)]) (1/(9n^2 )) +Σ_(n=0) ^([((19)/3)]) (1/((3k+1)^2 )) +Σ_(n=0) ^([((18)/3)]) (1/((3k+2)^2 )) =(1/9) Σ_(n=1) ^6 (1/n^2 ) +Σ_(n=0) ^6 (1/((3k+1)^2 )) +Σ_(n=0) ^6 (1/((3k+2)^2 )) =(1/9){ 1+(1/2^2 ) +(1/3^2 ) +(1/4^2 ) +(1/5^2 ) +(1/6^2 )} +{1+(1/4^2 ) +(1/7^2 ) +(1/(10^2 )) +(1/(13^2 )) +(1/(16^2 ))+(1/(19^2 ))} +{(1/2^2 ) +(1/5^2 ) +(1/8^2 ) +(1/(11^2 )) +(1/(14^2 )) +(1/(17^2 )) +(1/(20^2 ))} =....](https://www.tinkutara.com/question/Q74965.png)
$${another}\:{way}\:\:\:{let}\:\:{S}\:=\sum_{{n}=\mathrm{1}} ^{\mathrm{20}} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$${S}\:=\:\sum_{{n}=\mathrm{1}_{{n}=\mathrm{3}{k}} } ^{\mathrm{20}} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{1}_{{n}=\mathrm{3}{k}+\mathrm{1}} } ^{\mathrm{20}} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{1}_{{n}=\mathrm{3}{k}+\mathrm{2}} } ^{\mathrm{20}} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\left[\frac{\mathrm{20}}{\mathrm{3}}\right]} \:\frac{\mathrm{1}}{\mathrm{9}{n}^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\left[\frac{\mathrm{19}}{\mathrm{3}}\right]} \:\frac{\mathrm{1}}{\left(\mathrm{3}{k}+\mathrm{1}\right)^{\mathrm{2}} }\:\:+\sum_{{n}=\mathrm{0}} ^{\left[\frac{\mathrm{18}}{\mathrm{3}}\right]} \:\frac{\mathrm{1}}{\left(\mathrm{3}{k}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\:\sum_{{n}=\mathrm{1}} ^{\mathrm{6}} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\mathrm{6}} \:\frac{\mathrm{1}}{\left(\mathrm{3}{k}+\mathrm{1}\right)^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\mathrm{6}} \:\frac{\mathrm{1}}{\left(\mathrm{3}{k}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left\{\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{2}} }\right\}\:+\left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{10}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{13}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{16}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{19}^{\mathrm{2}} }\right\} \\ $$$$+\left\{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{8}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{14}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{17}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{20}^{\mathrm{2}} }\right\}\:=…. \\ $$$$ \\ $$
