Menu Close

Calculate-n-1-n-2-3-n-

Tinku Tara 0 Comments
Pin




Question Number 141791 by Chhing last updated on 23/May/21
Calculate Σ_(n=1) ^(+∞) (n^2 /3^n )
$$\mathrm{Calculate} \\ $$$$\:\underset{\mathrm{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\:\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{n}} } \\ $$
Answered by mr W last updated on 23/May/21
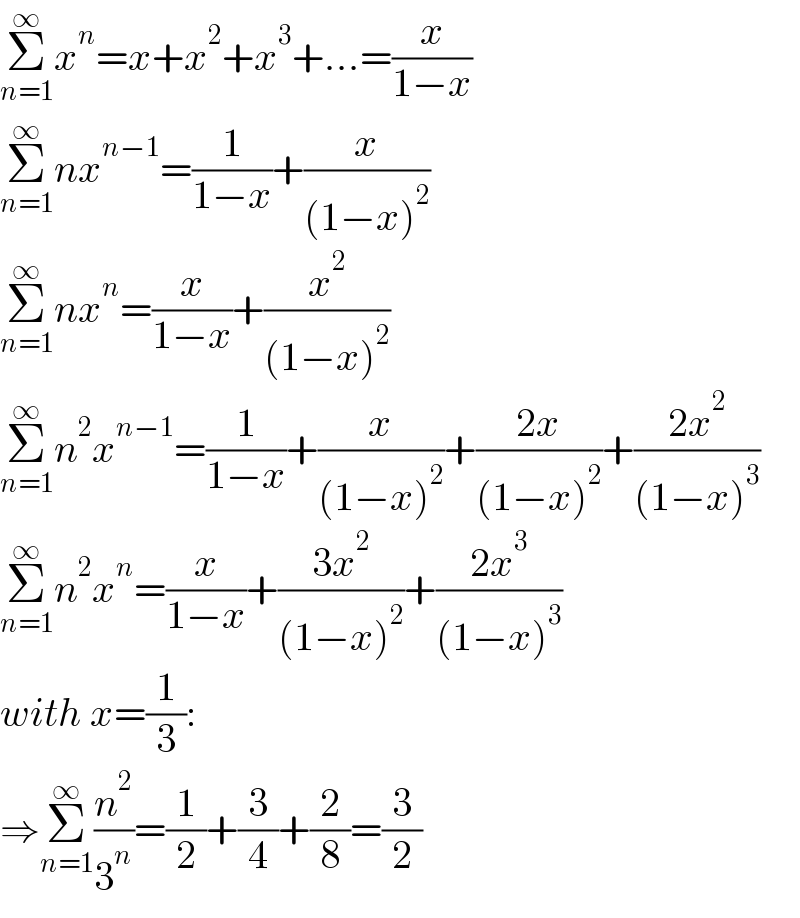
Σ_(n=1) ^∞ x^n =x+x^2 +x^3 +...=(x/(1−x)) Σ_(n=1) ^∞ nx^(n−1) =(1/(1−x))+(x/((1−x)^2 )) Σ_(n=1) ^∞ nx^n =(x/(1−x))+(x^2 /((1−x)^2 )) Σ_(n=1) ^∞ n^2 x^(n−1) =(1/(1−x))+(x/((1−x)^2 ))+((2x)/((1−x)^2 ))+((2x^2 )/((1−x)^3 )) Σ_(n=1) ^∞ n^2 x^n =(x/(1−x))+((3x^2 )/((1−x)^2 ))+((2x^3 )/((1−x)^3 )) with x=(1/3): ⇒Σ_(n=1) ^∞ (n^2 /3^n )=(1/2)+(3/4)+(2/8)=(3/2)
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{n}} ={x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…=\frac{{x}}{\mathrm{1}−{x}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{nx}^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}−{x}}+\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{nx}^{{n}} =\frac{{x}}{\mathrm{1}−{x}}+\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}^{\mathrm{2}} {x}^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}−{x}}+\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}^{\mathrm{2}} {x}^{{n}} =\frac{{x}}{\mathrm{1}−{x}}+\frac{\mathrm{3}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$${with}\:{x}=\frac{\mathrm{1}}{\mathrm{3}}: \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{2}} }{\mathrm{3}^{{n}} }=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{2}}{\mathrm{8}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by qaz last updated on 23/May/21
Σ_(n=1) ^∞ (n^2 /3^n )=Σ_(n=0) ^∞ (((n+1)^2 )/3^(n+1) )=(1/3)(xD+1)^2 ∣_(x=1/3) (1/(1−x)) =(1/3)[(xD)^2 +2xD+1]_(x=1/3) (1/(1−x)) =(1/3)(x^2 D^2 +3xD+1)∣_(x=1/3) (1/(1−x)) =(1/3)[((2x^2 )/((1−x)^3 ))+((3x)/((1−x)^2 ))+(1/(1−x))]_(x=1/3) =(1/3)((3/4)+(9/4)+(3/2)) =(3/2)
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{2}} }{\mathrm{3}^{{n}} }=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}^{{n}+\mathrm{1}} }=\frac{\mathrm{1}}{\mathrm{3}}\left({xD}+\mathrm{1}\right)^{\mathrm{2}} \mid_{{x}=\mathrm{1}/\mathrm{3}} \frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[\left({xD}\right)^{\mathrm{2}} +\mathrm{2}{xD}+\mathrm{1}\right]_{{x}=\mathrm{1}/\mathrm{3}} \frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left({x}^{\mathrm{2}} {D}^{\mathrm{2}} +\mathrm{3}{xD}+\mathrm{1}\right)\mid_{{x}=\mathrm{1}/\mathrm{3}} \frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }+\frac{\mathrm{3}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}−{x}}\right]_{{x}=\mathrm{1}/\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{9}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 23/May/21
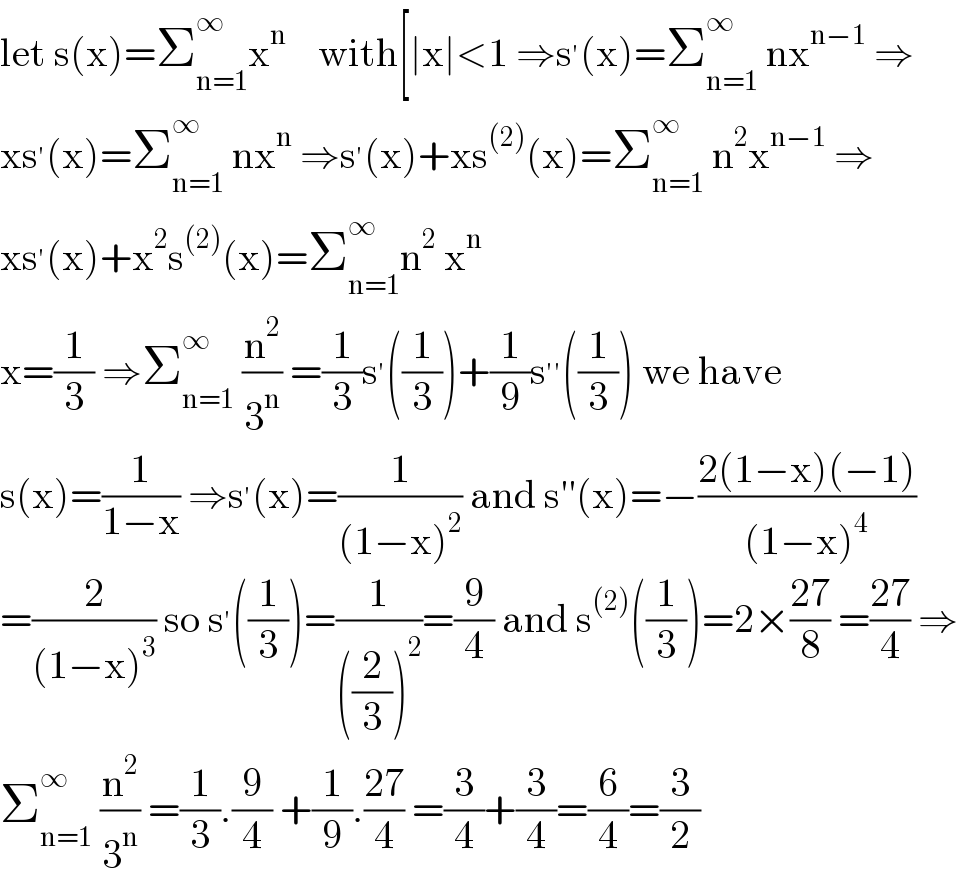
let s(x)=Σ_(n=1) ^∞ x^n with[∣x∣<1 ⇒s^′ (x)=Σ_(n=1) ^∞ nx^(n−1) ⇒ xs^′ (x)=Σ_(n=1) ^∞ nx^n ⇒s^′ (x)+xs^((2)) (x)=Σ_(n=1) ^∞ n^2 x^(n−1) ⇒ xs^′ (x)+x^2 s^((2)) (x)=Σ_(n=1) ^∞ n^2 x^n x=(1/3) ⇒Σ_(n=1) ^∞ (n^2 /3^n ) =(1/3)s^′ ((1/3))+(1/9)s^(′′) ((1/3)) we have s(x)=(1/(1−x)) ⇒s^′ (x)=(1/((1−x)^2 )) and s′′(x)=−((2(1−x)(−1))/((1−x)^4 )) =(2/((1−x)^3 )) so s^′ ((1/3))=(1/(((2/3))^2 ))=(9/4) and s^((2)) ((1/3))=2×((27)/8) =((27)/4) ⇒ Σ_(n=1) ^∞ (n^2 /3^n ) =(1/3).(9/4) +(1/9).((27)/4) =(3/4)+(3/4)=(6/4)=(3/2)
$$\mathrm{let}\:\mathrm{s}\left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \mathrm{x}^{\mathrm{n}} \:\:\:\:\mathrm{with}\left[\mid\mathrm{x}\mid<\mathrm{1}\:\Rightarrow\mathrm{s}^{'} \left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \:\Rightarrow\right. \\ $$$$\mathrm{xs}^{'} \left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}} \:\Rightarrow\mathrm{s}^{'} \left(\mathrm{x}\right)+\mathrm{xs}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}^{\mathrm{2}} \mathrm{x}^{\mathrm{n}−\mathrm{1}} \:\Rightarrow \\ $$$$\mathrm{xs}^{'} \left(\mathrm{x}\right)+\mathrm{x}^{\mathrm{2}} \mathrm{s}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \mathrm{n}^{\mathrm{2}} \:\mathrm{x}^{\mathrm{n}} \\ $$$$\mathrm{x}=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{n}} }\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{s}^{'} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{9}}\mathrm{s}^{''} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{s}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\:\Rightarrow\mathrm{s}^{'} \left(\mathrm{x}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:\mathrm{and}\:\mathrm{s}''\left(\mathrm{x}\right)=−\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{x}\right)\left(−\mathrm{1}\right)}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} }\:\mathrm{so}\:\mathrm{s}^{'} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\mathrm{9}}{\mathrm{4}}\:\mathrm{and}\:\mathrm{s}^{\left(\mathrm{2}\right)} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\mathrm{2}×\frac{\mathrm{27}}{\mathrm{8}}\:=\frac{\mathrm{27}}{\mathrm{4}}\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{n}} }\:=\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{9}}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{9}}.\frac{\mathrm{27}}{\mathrm{4}}\:=\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{6}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by qaz last updated on 23/May/21
Σ_(n=0) ^∞ (((n+1)^2 )/3^(n+1) )=Σ_(n=0) ^∞ (((n+1)^2 )/(Γ(n+1)))∫_0 ^∞ u^n e^(−3u) du =∫_0 ^∞ e^(−3u) Σ_(n=0) ^∞ (((n+1)^2 )/(n!))u^n du =∫_0 ^∞ e^(−3u) (xD+1)^2 ∣_(x=u) Σ_(n=0) ^∞ (x^n /(n!))du =∫_0 ^∞ e^(−3u) (x^2 D^2 +3xD+1)∣_(x=u) e^x du =∫_0 ^∞ e^(−3u) (x^2 +3x+1)e^x ∣_(x=u) du =∫_0 ^∞ e^(−2u) (u^2 +3u+1)du =(2/2^3 )+(3/2^2 )+(1/2) =(3/2) i have found another intresting way.
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}^{{n}+\mathrm{1}} }=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\Gamma\left({n}+\mathrm{1}\right)}\int_{\mathrm{0}} ^{\infty} {u}^{{n}} {e}^{−\mathrm{3}{u}} {du} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{3}{u}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{{n}!}{u}^{{n}} {du} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{3}{u}} \left({xD}+\mathrm{1}\right)^{\mathrm{2}} \mid_{{x}={u}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!}{du} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{3}{u}} \left({x}^{\mathrm{2}} {D}^{\mathrm{2}} +\mathrm{3}{xD}+\mathrm{1}\right)\mid_{{x}={u}} {e}^{{x}} {du} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{3}{u}} \left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right){e}^{{x}} \mid_{{x}={u}} {du} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{u}} \left({u}^{\mathrm{2}} +\mathrm{3}{u}+\mathrm{1}\right){du} \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${i}\:{have}\:{found}\:\:{another}\:{intresting}\:{way}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *