Question Number 76790 by john santu last updated on 30/Dec/19
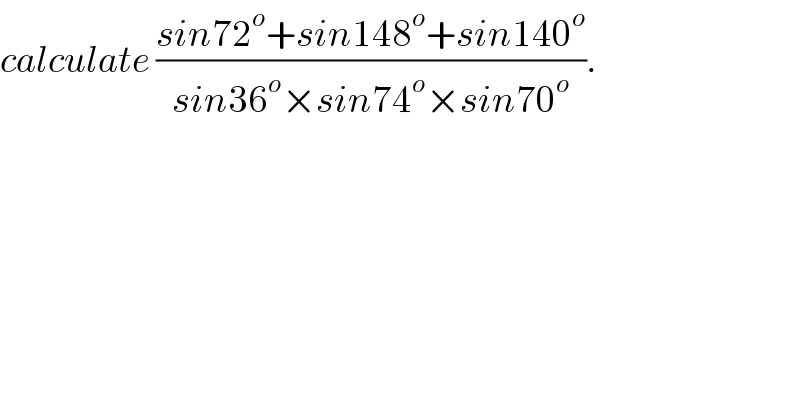
$${calculate}\:\frac{{sin}\mathrm{72}^{{o}} +{sin}\mathrm{148}^{{o}} +{sin}\mathrm{140}^{{o}} }{{sin}\mathrm{36}^{{o}} ×{sin}\mathrm{74}^{{o}} ×{sin}\mathrm{70}^{{o}} }. \\ $$
Commented by benjo 1/2 santuyy last updated on 31/Dec/19
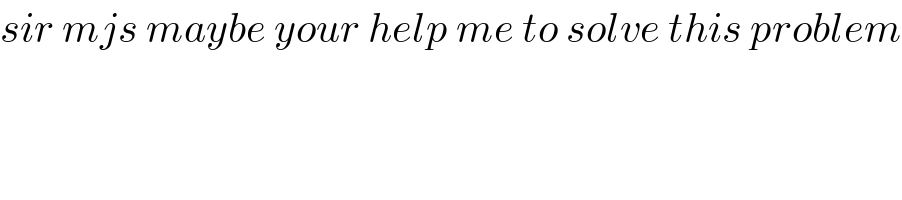
$${sir}\:{mjs}\:{maybe}\:{your}\:{help}\:{me}\:{to}\:{solve}\:{this}\:{problem} \\ $$
Answered by benjo 1/2 santuyy last updated on 30/Dec/19
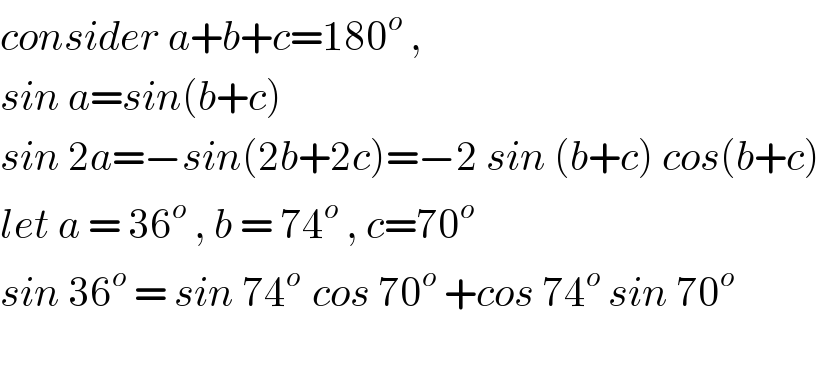
$${consider}\:{a}+{b}+{c}=\mathrm{180}^{{o}} \:,\: \\ $$$${sin}\:{a}={sin}\left({b}+{c}\right) \\ $$$${sin}\:\mathrm{2}{a}=−{sin}\left(\mathrm{2}{b}+\mathrm{2}{c}\right)=−\mathrm{2}\:{sin}\:\left({b}+{c}\right)\:{cos}\left({b}+{c}\right) \\ $$$${let}\:{a}\:=\:\mathrm{36}^{{o}} \:,\:{b}\:=\:\mathrm{74}^{{o}} \:,\:{c}=\mathrm{70}^{{o}\:} \\ $$$${sin}\:\mathrm{36}^{{o}} \:=\:{sin}\:\mathrm{74}^{{o}\:} \:{cos}\:\mathrm{70}^{{o}} \:+{cos}\:\mathrm{74}^{{o}} \:{sin}\:\mathrm{70}^{{o}} \\ $$$$ \\ $$
Answered by benjo 1/2 santuyy last updated on 30/Dec/19

$$\mathrm{4}\:{sir}? \\ $$
Answered by mind is power last updated on 27/Feb/20
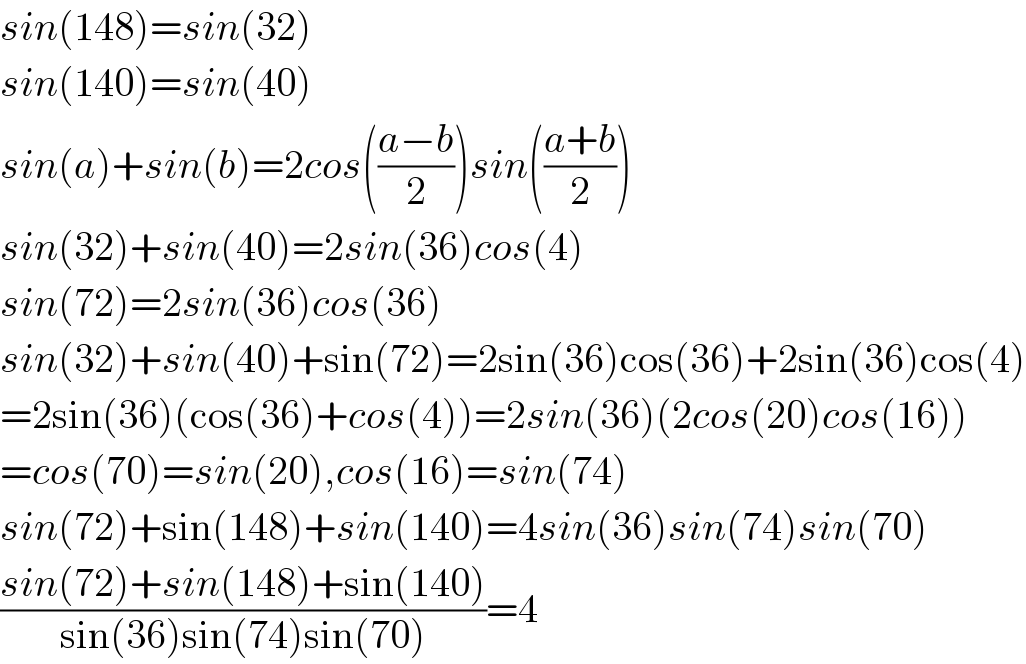
$${sin}\left(\mathrm{148}\right)={sin}\left(\mathrm{32}\right) \\ $$$${sin}\left(\mathrm{140}\right)={sin}\left(\mathrm{40}\right) \\ $$$${sin}\left({a}\right)+{sin}\left({b}\right)=\mathrm{2}{cos}\left(\frac{{a}−{b}}{\mathrm{2}}\right){sin}\left(\frac{{a}+{b}}{\mathrm{2}}\right) \\ $$$${sin}\left(\mathrm{32}\right)+{sin}\left(\mathrm{40}\right)=\mathrm{2}{sin}\left(\mathrm{36}\right){cos}\left(\mathrm{4}\right) \\ $$$${sin}\left(\mathrm{72}\right)=\mathrm{2}{sin}\left(\mathrm{36}\right){cos}\left(\mathrm{36}\right) \\ $$$${sin}\left(\mathrm{32}\right)+{sin}\left(\mathrm{40}\right)+\mathrm{sin}\left(\mathrm{72}\right)=\mathrm{2sin}\left(\mathrm{36}\right)\mathrm{cos}\left(\mathrm{36}\right)+\mathrm{2sin}\left(\mathrm{36}\right)\mathrm{cos}\left(\mathrm{4}\right) \\ $$$$=\mathrm{2sin}\left(\mathrm{36}\right)\left(\mathrm{cos}\left(\mathrm{36}\right)+{cos}\left(\mathrm{4}\right)\right)=\mathrm{2}{sin}\left(\mathrm{36}\right)\left(\mathrm{2}{cos}\left(\mathrm{20}\right){cos}\left(\mathrm{16}\right)\right) \\ $$$$={cos}\left(\mathrm{70}\right)={sin}\left(\mathrm{20}\right),{cos}\left(\mathrm{16}\right)={sin}\left(\mathrm{74}\right) \\ $$$${sin}\left(\mathrm{72}\right)+\mathrm{sin}\left(\mathrm{148}\right)+{sin}\left(\mathrm{140}\right)=\mathrm{4}{sin}\left(\mathrm{36}\right){sin}\left(\mathrm{74}\right){sin}\left(\mathrm{70}\right) \\ $$$$\frac{{sin}\left(\mathrm{72}\right)+{sin}\left(\mathrm{148}\right)+\mathrm{sin}\left(\mathrm{140}\right)}{\mathrm{sin}\left(\mathrm{36}\right)\mathrm{sin}\left(\mathrm{74}\right)\mathrm{sin}\left(\mathrm{70}\right)}=\mathrm{4} \\ $$
