Menu Close

Calculate-the-lim-x-1-x-x-x-x-x-x-

Tinku Tara 0 Comments
Pin




Question Number 141077 by Opredador last updated on 15/May/21
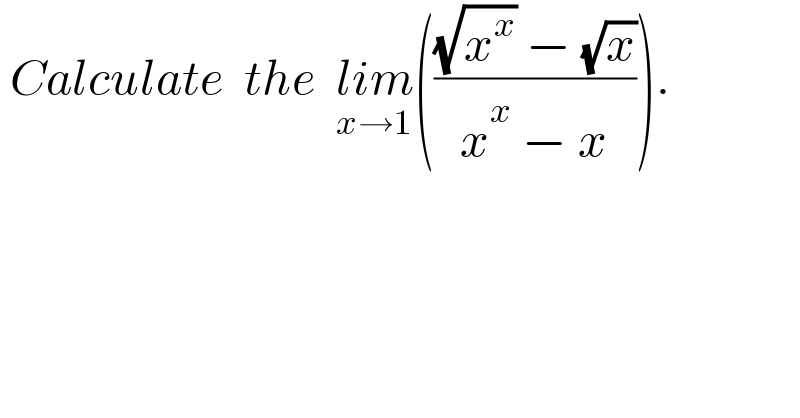
Calculate the lim_(x→1) ((((√x^x ) − (√x))/(x^x − x))).
$$\:{Calculate}\:\:{the}\:\:\underset{{x}\rightarrow\mathrm{1}} {{lim}}\left(\frac{\sqrt{{x}^{{x}} }\:−\:\sqrt{{x}}}{{x}^{{x}} \:−\:{x}}\right). \\ $$
Answered by EDWIN88 last updated on 15/May/21
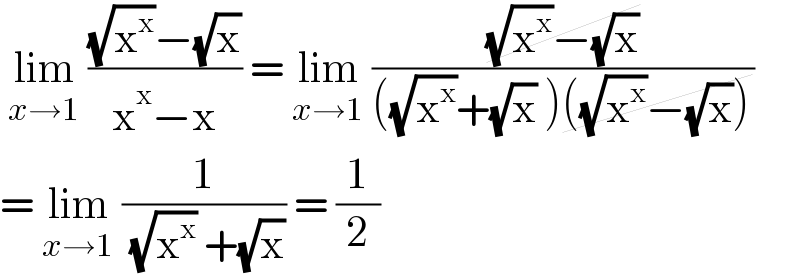
lim_(x→1) (((√x^x )−(√x))/(x^x −x)) = lim_(x→1) (((√x^x )−(√x))/(((√x^x )+(√x) )((√x^x )−(√x)))) = lim_(x→1) (1/( (√x^x ) +(√x))) = (1/2)
$$\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{x}^{\mathrm{x}} }−\sqrt{\mathrm{x}}}{\mathrm{x}^{\mathrm{x}} −\mathrm{x}}\:=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\cancel{\sqrt{\mathrm{x}^{\mathrm{x}} }−\sqrt{\mathrm{x}}}}{\left(\sqrt{\mathrm{x}^{\mathrm{x}} }+\sqrt{\mathrm{x}}\:\right)\cancel{\left(\sqrt{\mathrm{x}^{\mathrm{x}} }−\sqrt{\mathrm{x}}\right)}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{x}} }\:+\sqrt{\mathrm{x}}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by EDWIN88 last updated on 15/May/21
Danke nochmal
$$ \\ $$ Danke nochmal
Commented by Opredador last updated on 15/May/21
Gracias
$$\:\mathrm{Gracias} \\ $$
Answered by mathmax by abdo last updated on 16/May/21
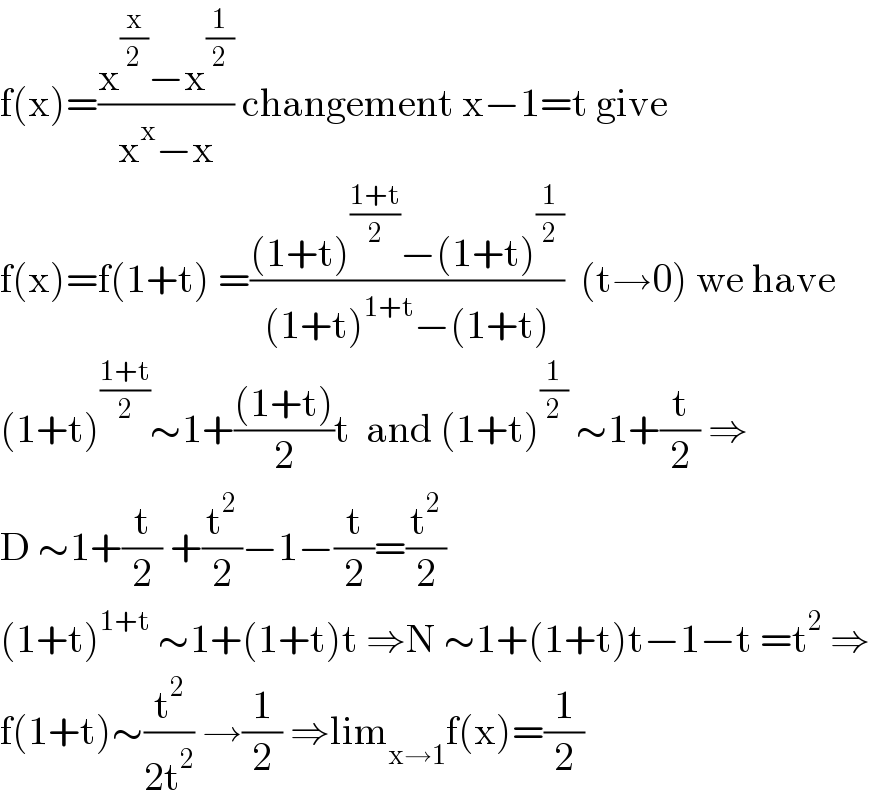
f(x)=((x^(x/2) −x^(1/2) )/(x^x −x)) changement x−1=t give f(x)=f(1+t) =(((1+t)^((1+t)/2) −(1+t)^(1/2) )/((1+t)^(1+t) −(1+t))) (t→0) we have (1+t)^((1+t)/2) ∼1+(((1+t))/2)t and (1+t)^(1/2) ∼1+(t/2) ⇒ D ∼1+(t/2) +(t^2 /2)−1−(t/2)=(t^2 /2) (1+t)^(1+t) ∼1+(1+t)t ⇒N ∼1+(1+t)t−1−t =t^2 ⇒ f(1+t)∼(t^2 /(2t^2 )) →(1/2) ⇒lim_(x→1) f(x)=(1/2)
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\frac{\mathrm{x}}{\mathrm{2}}} −\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{x}^{\mathrm{x}} −\mathrm{x}}\:\mathrm{changement}\:\mathrm{x}−\mathrm{1}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{1}+\mathrm{t}\right)\:=\frac{\left(\mathrm{1}+\mathrm{t}\right)^{\frac{\mathrm{1}+\mathrm{t}}{\mathrm{2}}} −\left(\mathrm{1}+\mathrm{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{1}+\mathrm{t}} −\left(\mathrm{1}+\mathrm{t}\right)}\:\:\left(\mathrm{t}\rightarrow\mathrm{0}\right)\:\mathrm{we}\:\mathrm{have} \\ $$$$\left(\mathrm{1}+\mathrm{t}\right)^{\frac{\mathrm{1}+\mathrm{t}}{\mathrm{2}}} \sim\mathrm{1}+\frac{\left(\mathrm{1}+\mathrm{t}\right)}{\mathrm{2}}\mathrm{t}\:\:\mathrm{and}\:\left(\mathrm{1}+\mathrm{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\sim\mathrm{1}+\frac{\mathrm{t}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{D}\:\sim\mathrm{1}+\frac{\mathrm{t}}{\mathrm{2}}\:+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}−\frac{\mathrm{t}}{\mathrm{2}}=\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{1}+\mathrm{t}} \:\sim\mathrm{1}+\left(\mathrm{1}+\mathrm{t}\right)\mathrm{t}\:\Rightarrow\mathrm{N}\:\sim\mathrm{1}+\left(\mathrm{1}+\mathrm{t}\right)\mathrm{t}−\mathrm{1}−\mathrm{t}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{1}+\mathrm{t}\right)\sim\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2t}^{\mathrm{2}} }\:\rightarrow\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *