Question Number 66800 by mathmax by abdo last updated on 19/Aug/19
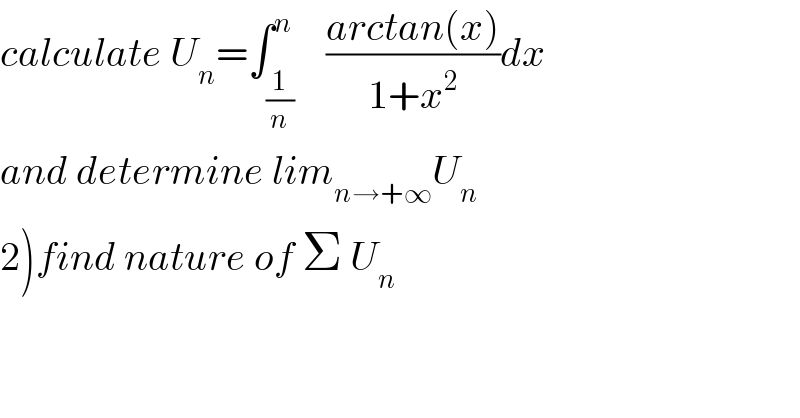
$${calculate}\:{U}_{{n}} =\int_{\frac{\mathrm{1}}{{n}}} ^{{n}} \:\:\:\frac{{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${and}\:{determine}\:{lim}_{{n}\rightarrow+\infty} {U}_{{n}} \\ $$$$\left.\mathrm{2}\right){find}\:{nature}\:{of}\:\Sigma\:{U}_{{n}} \\ $$
Commented by mathmax by abdo last updated on 21/Aug/19
![1) by parts u^′ =(1/(1+x^2 )) and v=arctanx ⇒ U_n =[ arctan^2 x]_(1/n) ^n −∫_(1/n) ^n arctan(x)(dx/(1+x^2 )) =arctan^2 (n)−arctan^2 ((1/n)) −U_n ⇒2U_n =arctan^2 (n)−arctan^2 ((1/n)) ⇒ U_n =(1/2){arctan^2 (n)−arctan^2 ((1/n))} ⇒lim_(n→+∞) U_n =(1/2)((π/2))^2 =(π^2 /8) 2) we have lim_(n→+∞) U_n ≠0 ⇒Σ U_n diverges.](https://www.tinkutara.com/question/Q66998.png)
$$\left.\mathrm{1}\right)\:{by}\:{parts}\:\:{u}^{'} =\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{and}\:{v}={arctanx}\:\Rightarrow \\ $$$${U}_{{n}} =\left[\:{arctan}^{\mathrm{2}} {x}\right]_{\frac{\mathrm{1}}{{n}}} ^{{n}} \:−\int_{\frac{\mathrm{1}}{{n}}} ^{{n}} {arctan}\left({x}\right)\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:={arctan}^{\mathrm{2}} \left({n}\right)−{arctan}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{n}}\right) \\ $$$$−{U}_{{n}} \:\Rightarrow\mathrm{2}{U}_{{n}} ={arctan}^{\mathrm{2}} \left({n}\right)−{arctan}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{n}}\right)\:\Rightarrow \\ $$$${U}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{{arctan}^{\mathrm{2}} \left({n}\right)−{arctan}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{n}}\right)\right\}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} {U}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{lim}_{{n}\rightarrow+\infty} {U}_{{n}} \neq\mathrm{0}\:\Rightarrow\Sigma\:{U}_{{n}} \:{diverges}. \\ $$
