Question Number 73034 by mathmax by abdo last updated on 05/Nov/19
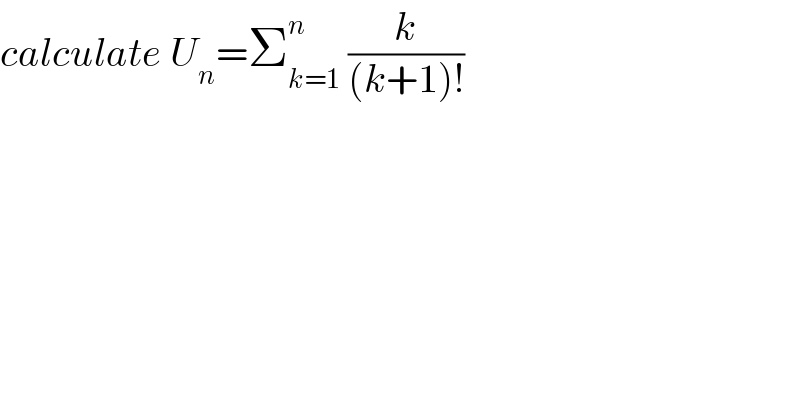
$${calculate}\:{U}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}}{\left({k}+\mathrm{1}\right)!} \\ $$
Commented by mathmax by abdo last updated on 06/Nov/19
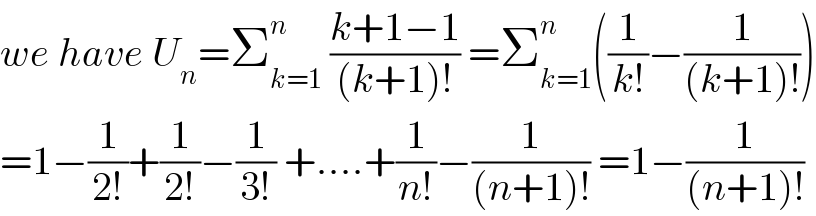
$${we}\:{have}\:{U}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}+\mathrm{1}−\mathrm{1}}{\left({k}+\mathrm{1}\right)!}\:=\sum_{{k}=\mathrm{1}} ^{{n}} \left(\frac{\mathrm{1}}{{k}!}−\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)!}\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}\:+….+\frac{\mathrm{1}}{{n}!}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!}\:=\mathrm{1}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!} \\ $$
Answered by mind is power last updated on 05/Nov/19

$$\mathrm{Un}=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}!}−\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)!}=\mathrm{1}−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!} \\ $$
