Menu Close

calculate-x-1-x-3-x-2-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 74886 by abdomathmax last updated on 03/Dec/19
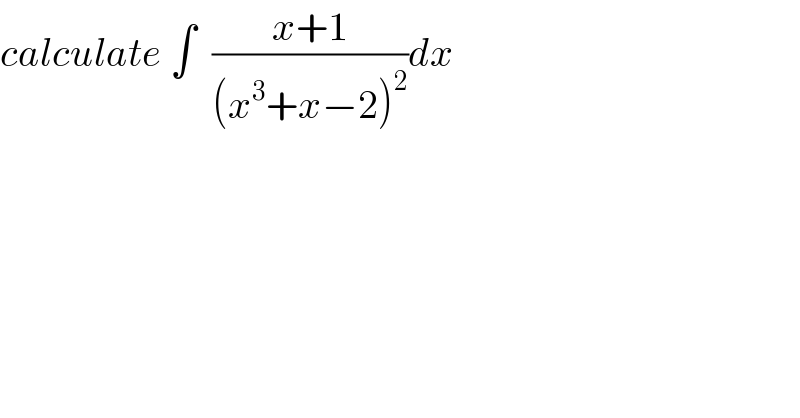
calculate ∫ ((x+1)/((x^3 +x−2)^2 ))dx
$${calculate}\:\int\:\:\frac{{x}+\mathrm{1}}{\left({x}^{\mathrm{3}} +{x}−\mathrm{2}\right)^{\mathrm{2}} }{dx} \\ $$
Commented by mathmax by abdo last updated on 15/Dec/19
let I =∫ ((x+1)/((x^3 +x−2)^2 ))dx let decompose F(x)=((x+1)/((x^3 +x−2)^2 )) we have x^3 +x−2 =x^3 −1 +x−1 =(x−1)(x^2 +x+1)+x−1 =(x−1)(x^2 +x+2) ⇒F(x)=((x+1)/((x−1)^2 (x^2 +x+2)^2 )) =(a/(x−1)) +(b/((x−1)^2 )) +((cx+d)/(x^2 +x+2)) +((ex +f)/((x^2 +x+2)^2 )) b=(x−1)^2 F(x)∣_(x=1) =(2/4^2 ) =(1/8) lim_(x→+∞) xF(x)=0=a+c ⇒c=−a ⇒ F(x)=(a/(x−1)) +(1/(8(x−1)^2 )) +((−ax+d)/(x^2 +x+2)) +((ex +f)/((x^2 +x+2)^2 )) F(0)=(1/4) =−a+(1/8) +(d/2) +(f/4) ⇒ 1=−4a+(1/2) +2d +f ⇒−4a+2d+f =(1/2) F(2)=(3/(64)) =a +(1/8) +((−2a+d)/8) +((2e +f)/(64)) ⇒ 3 =64a +8 +8(−2a+d)+2e+f ⇒3=48a +8 +8d +2e+f ⇒ ⇒48a+8d+2e+f =−5 we form a system with 4 equation with unknown a ,d ,e and f to get the value any way we get I =aln∣x−1∣−(1/(8(x−1))) +∫((−ax+d)/(x^2 )x+2))dx +∫ ((ex+f)/((x^2 +x+2)^2 )) ...be continued...
$${let}\:{I}\:=\int\:\:\frac{{x}+\mathrm{1}}{\left({x}^{\mathrm{3}} +{x}−\mathrm{2}\right)^{\mathrm{2}} }{dx}\:{let}\:{decompose}\:{F}\left({x}\right)=\frac{{x}+\mathrm{1}}{\left({x}^{\mathrm{3}} +{x}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${we}\:{have}\:{x}^{\mathrm{3}} \:+{x}−\mathrm{2}\:={x}^{\mathrm{3}} −\mathrm{1}\:+{x}−\mathrm{1}\:=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)+{x}−\mathrm{1} \\ $$$$=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{2}\right)\:\Rightarrow{F}\left({x}\right)=\frac{{x}+\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +{x}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$=\frac{{a}}{{x}−\mathrm{1}}\:+\frac{{b}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{cx}+{d}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{2}}\:+\frac{{ex}\:+{f}}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${b}=\left({x}−\mathrm{1}\right)^{\mathrm{2}} {F}\left({x}\right)\mid_{{x}=\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{4}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)=\mathrm{0}={a}+{c}\:\Rightarrow{c}=−{a}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}−\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{8}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{−{ax}+{d}}{{x}^{\mathrm{2}} +{x}+\mathrm{2}}\:+\frac{{ex}\:+{f}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{4}}\:=−{a}+\frac{\mathrm{1}}{\mathrm{8}}\:+\frac{{d}}{\mathrm{2}}\:+\frac{{f}}{\mathrm{4}}\:\Rightarrow \\ $$$$\mathrm{1}=−\mathrm{4}{a}+\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{2}{d}\:+{f}\:\Rightarrow−\mathrm{4}{a}+\mathrm{2}{d}+{f}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${F}\left(\mathrm{2}\right)=\frac{\mathrm{3}}{\mathrm{64}}\:={a}\:+\frac{\mathrm{1}}{\mathrm{8}}\:+\frac{−\mathrm{2}{a}+{d}}{\mathrm{8}}\:+\frac{\mathrm{2}{e}\:+{f}}{\mathrm{64}}\:\Rightarrow \\ $$$$\mathrm{3}\:=\mathrm{64}{a}\:+\mathrm{8}\:+\mathrm{8}\left(−\mathrm{2}{a}+{d}\right)+\mathrm{2}{e}+{f}\:\Rightarrow\mathrm{3}=\mathrm{48}{a}\:+\mathrm{8}\:+\mathrm{8}{d}\:+\mathrm{2}{e}+{f}\:\Rightarrow \\ $$$$\Rightarrow\mathrm{48}{a}+\mathrm{8}{d}+\mathrm{2}{e}+{f}\:=−\mathrm{5} \\ $$$${we}\:{form}\:{a}\:{system}\:{with}\:\mathrm{4}\:{equation}\:{with}\:{unknown}\:{a}\:,{d}\:,{e}\:{and}\:{f} \\ $$$${to}\:{get}\:{the}\:{value}\:{any}\:{way}\:\:{we}\:{get} \\ $$$${I}\:={aln}\mid{x}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{8}\left({x}−\mathrm{1}\right)}\:+\int\frac{−{ax}+{d}}{\left.{x}^{\mathrm{2}} \:\right){x}+\mathrm{2}}{dx}\:+\int\:\:\frac{{ex}+{f}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$…{be}\:{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *