Menu Close

calculate-x-2-x-3-x-3-x-2-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 74344 by mathmax by abdo last updated on 22/Nov/19
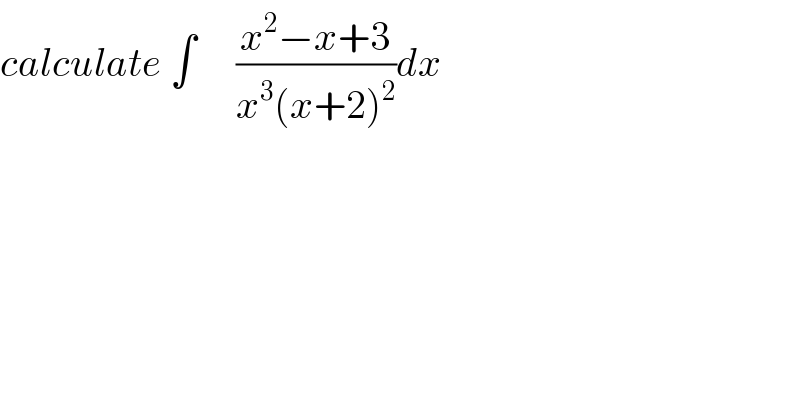
calculate ∫ ((x^2 −x+3)/(x^3 (x+2)^2 ))dx
$${calculate}\:\int\:\:\:\:\:\frac{{x}^{\mathrm{2}} −{x}+\mathrm{3}}{{x}^{\mathrm{3}} \left({x}+\mathrm{2}\right)^{\mathrm{2}} }{dx} \\ $$
Commented by mathmax by abdo last updated on 24/Nov/19
let I=∫ ((x^2 −x+3)/(x^3 (x+2)^2 ))dx decompose F(x)=((x^2 −x+3)/(x^3 (x+2)^2 )) F(x)=(a/x)+(b/x^2 ) +(c/x^3 ) +(d/(x+2)) +(e/((x+2)^2 )) c =x^3 F(x)∣_(x=0) =(3/4) and e=(x+2)^2 F(x)∣_(x=−2) =((4+2+3)/(−8)) =−(9/8) F(x)=(a/x)+(b/x^2 ) +(3/(4x^3 )) +(d/(x+2))−(9/(8(x+2)^2 )) lim_(x→+∞) xF(x)=0=a+d ⇒d=−a ⇒ F(x)=(a/x)+(b/x^2 )+(3/(4x^3 ))−(a/(x+2))−(9/(8(x+2)^2 )) F(−1)=−5 =−a+b−(3/4) −a−(9/8) =−2a−((15)/8) +b ⇒ 2a−b+((15)/8) =5 ⇒2a−b =5−((15)/8) =((25)/8) F(1)=(3/9)=(1/3) =a+b+(3/4)−(a/3)−(1/8) ⇒ 1=3a+3b+(9/4)−a−(3/8) =2a+3b +((15)/8) ⇒2a+3b =1−((15)/8) =−(7/8) we have b=2a−((25)/8) ⇒2a+3(2a−((25)/8))=−(7/8) ⇒ 8a −((75)/8)=−(7/8) ⇒8a =((75−7)/8) =((68)/8) =((34)/4) =((17)/2) ⇒a=((17)/(16)) b=((17)/8)−((25)/8) =−1 ⇒F(x)=((17)/(16x))−(1/x^2 )+(3/(4x^3 ))−((17)/(16(x+2)))−(9/(8(x+2)^2 )) ⇒ I =((17)/(16))ln∣x∣+(1/x)−(3/(8x^2 ))−((17)/(16))ln∣x+2∣+(9/(8(x+2))) +C
$${let}\:{I}=\int\:\frac{{x}^{\mathrm{2}} −{x}+\mathrm{3}}{{x}^{\mathrm{3}} \left({x}+\mathrm{2}\right)^{\mathrm{2}} }{dx}\:\:{decompose}\:{F}\left({x}\right)=\frac{{x}^{\mathrm{2}} −{x}+\mathrm{3}}{{x}^{\mathrm{3}} \left({x}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}}+\frac{{b}}{{x}^{\mathrm{2}} }\:+\frac{{c}}{{x}^{\mathrm{3}} }\:+\frac{{d}}{{x}+\mathrm{2}}\:+\frac{{e}}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${c}\:={x}^{\mathrm{3}} {F}\left({x}\right)\mid_{{x}=\mathrm{0}} \:\:\:=\frac{\mathrm{3}}{\mathrm{4}}\:\:{and}\:{e}=\left({x}+\mathrm{2}\overset{\mathrm{2}} {\right)}\:{F}\left({x}\right)\mid_{{x}=−\mathrm{2}} =\frac{\mathrm{4}+\mathrm{2}+\mathrm{3}}{−\mathrm{8}}\:=−\frac{\mathrm{9}}{\mathrm{8}} \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}}+\frac{{b}}{{x}^{\mathrm{2}} }\:+\frac{\mathrm{3}}{\mathrm{4}{x}^{\mathrm{3}} }\:+\frac{{d}}{{x}+\mathrm{2}}−\frac{\mathrm{9}}{\mathrm{8}\left({x}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)=\mathrm{0}={a}+{d}\:\Rightarrow{d}=−{a}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}}+\frac{{b}}{{x}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{4}{x}^{\mathrm{3}} }−\frac{{a}}{{x}+\mathrm{2}}−\frac{\mathrm{9}}{\mathrm{8}\left({x}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${F}\left(−\mathrm{1}\right)=−\mathrm{5}\:=−{a}+{b}−\frac{\mathrm{3}}{\mathrm{4}}\:−{a}−\frac{\mathrm{9}}{\mathrm{8}}\:=−\mathrm{2}{a}−\frac{\mathrm{15}}{\mathrm{8}}\:+{b}\:\Rightarrow \\ $$$$\mathrm{2}{a}−{b}+\frac{\mathrm{15}}{\mathrm{8}}\:=\mathrm{5}\:\Rightarrow\mathrm{2}{a}−{b}\:=\mathrm{5}−\frac{\mathrm{15}}{\mathrm{8}}\:=\frac{\mathrm{25}}{\mathrm{8}} \\ $$$${F}\left(\mathrm{1}\right)=\frac{\mathrm{3}}{\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{3}}\:={a}+{b}+\frac{\mathrm{3}}{\mathrm{4}}−\frac{{a}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{8}}\:\Rightarrow \\ $$$$\mathrm{1}=\mathrm{3}{a}+\mathrm{3}{b}+\frac{\mathrm{9}}{\mathrm{4}}−{a}−\frac{\mathrm{3}}{\mathrm{8}}\:=\mathrm{2}{a}+\mathrm{3}{b}\:+\frac{\mathrm{15}}{\mathrm{8}}\:\Rightarrow\mathrm{2}{a}+\mathrm{3}{b}\:=\mathrm{1}−\frac{\mathrm{15}}{\mathrm{8}}\:=−\frac{\mathrm{7}}{\mathrm{8}} \\ $$$${we}\:{have}\:{b}=\mathrm{2}{a}−\frac{\mathrm{25}}{\mathrm{8}}\:\Rightarrow\mathrm{2}{a}+\mathrm{3}\left(\mathrm{2}{a}−\frac{\mathrm{25}}{\mathrm{8}}\right)=−\frac{\mathrm{7}}{\mathrm{8}}\:\Rightarrow \\ $$$$\mathrm{8}{a}\:−\frac{\mathrm{75}}{\mathrm{8}}=−\frac{\mathrm{7}}{\mathrm{8}}\:\Rightarrow\mathrm{8}{a}\:=\frac{\mathrm{75}−\mathrm{7}}{\mathrm{8}}\:=\frac{\mathrm{68}}{\mathrm{8}}\:=\frac{\mathrm{34}}{\mathrm{4}}\:=\frac{\mathrm{17}}{\mathrm{2}}\:\Rightarrow{a}=\frac{\mathrm{17}}{\mathrm{16}} \\ $$$${b}=\frac{\mathrm{17}}{\mathrm{8}}−\frac{\mathrm{25}}{\mathrm{8}}\:=−\mathrm{1} \\ $$$$\:\Rightarrow{F}\left({x}\right)=\frac{\mathrm{17}}{\mathrm{16}{x}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{4}{x}^{\mathrm{3}} }−\frac{\mathrm{17}}{\mathrm{16}\left({x}+\mathrm{2}\right)}−\frac{\mathrm{9}}{\mathrm{8}\left({x}+\mathrm{2}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{17}}{\mathrm{16}}{ln}\mid{x}\mid+\frac{\mathrm{1}}{{x}}−\frac{\mathrm{3}}{\mathrm{8}{x}^{\mathrm{2}} }−\frac{\mathrm{17}}{\mathrm{16}}{ln}\mid{x}+\mathrm{2}\mid+\frac{\mathrm{9}}{\mathrm{8}\left({x}+\mathrm{2}\right)}\:+{C} \\ $$$$ \\ $$
Answered by MJS last updated on 24/Nov/19
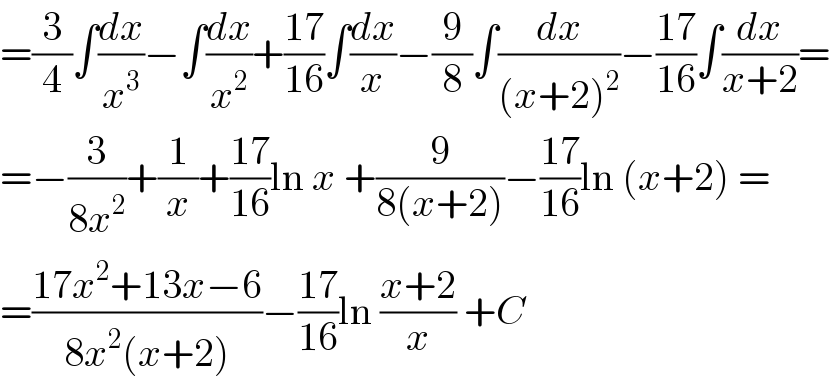
=(3/4)∫(dx/x^3 )−∫(dx/x^2 )+((17)/(16))∫(dx/x)−(9/8)∫(dx/((x+2)^2 ))−((17)/(16))∫(dx/(x+2))= =−(3/(8x^2 ))+(1/x)+((17)/(16))ln x +(9/(8(x+2)))−((17)/(16))ln (x+2) = =((17x^2 +13x−6)/(8x^2 (x+2)))−((17)/(16))ln ((x+2)/x) +C
$$=\frac{\mathrm{3}}{\mathrm{4}}\int\frac{{dx}}{{x}^{\mathrm{3}} }−\int\frac{{dx}}{{x}^{\mathrm{2}} }+\frac{\mathrm{17}}{\mathrm{16}}\int\frac{{dx}}{{x}}−\frac{\mathrm{9}}{\mathrm{8}}\int\frac{{dx}}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} }−\frac{\mathrm{17}}{\mathrm{16}}\int\frac{{dx}}{{x}+\mathrm{2}}= \\ $$$$=−\frac{\mathrm{3}}{\mathrm{8}{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{17}}{\mathrm{16}}\mathrm{ln}\:{x}\:+\frac{\mathrm{9}}{\mathrm{8}\left({x}+\mathrm{2}\right)}−\frac{\mathrm{17}}{\mathrm{16}}\mathrm{ln}\:\left({x}+\mathrm{2}\right)\:= \\ $$$$=\frac{\mathrm{17}{x}^{\mathrm{2}} +\mathrm{13}{x}−\mathrm{6}}{\mathrm{8}{x}^{\mathrm{2}} \left({x}+\mathrm{2}\right)}−\frac{\mathrm{17}}{\mathrm{16}}\mathrm{ln}\:\frac{{x}+\mathrm{2}}{{x}}\:+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *