Menu Close

calculte-sin-pix-2-x-2-2x-2-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 137536 by Mathspace last updated on 03/Apr/21
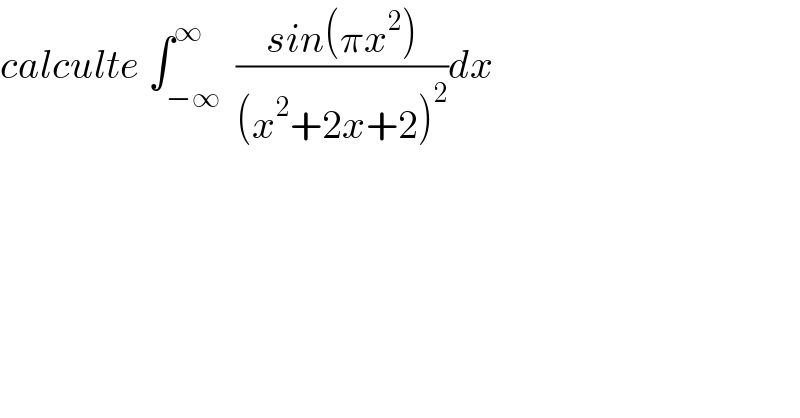
calculte ∫_(−∞) ^∞ ((sin(πx^2 ))/((x^2 +2x+2)^2 ))dx
$${calculte}\:\int_{−\infty} ^{\infty} \:\frac{{sin}\left(\pi{x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }{dx} \\ $$
Answered by mathmax by abdo last updated on 04/Apr/21
let f(a)=∫_(−∞) ^(+∞) ((sin(πx^2 ))/(x^2 +2x+a))dx with a>1 we have f^′ (a)=−∫_(−∞) ^(+∞) ((sin(πx^2 ))/((x^2 +2x+a)^2 )) ⇒f^′ (2)=−∫_(−∞) ^(+∞) ((sin(πx^2 ))/((x^2 +2x+2)^2 )) ⇒ ∫_(−∞) ^(+∞) ((sin(πx^2 ))/((x^2 +2x+2)^2 ))=−f^′ (2) we have f(a)=Im(∫_(−∞) ^(+∞) (e^(iπx^2 ) /(x^2 +2x+a))dx) let ϕ(z)=(e^(iπz^2 ) /(z^2 +2z+a)) poles of ϕ? Δ^′ =1−a<0 ⇒z_1 =−1+i(√(a−1)) and z_2 =−1−i(√(a−1)) ϕ(z)=(e^(iπz^2 ) /((z−z_1 )(z−z_2 ))) residus theorem ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,z_1 ) =2iπ×(e^(iπz_1 ^2 ) /(2i(√(a−1)))) =(π/( (√(a−1)))) e^(iπ{1−2i(√(a−1))−a+1)) =(π/( (√(a−1)))) e^(iπ{2−a−2i(√(a−1))}) =(π/( (√(a−1)))) e^(iπ(2−a)) .e^(2π(√(a−1))) =((πe^(2π(√(a−1))) )/( (√(a−1)))){cos(π(2−a))+isin(π(2−a))} ⇒ f(a)=−((π e^(2π(√(a−1))) )/( (√(a−1)))).sin(πa) ⇒ −f^′ (a) =π((e^(2π(√(a−1))) /( (√(a−1)))))^, sin(πa) +π^2 cos(πa).(e^(2π(√(a−1))) /( (√(a−1)))) but ((e^(2π(√(a−1))) /( (√(a−1)))))^′ =((((2π)/(2(√(a−1))))e^(2π(√(a−1))) .(√(a−1))−e^(2π(√(a−1))) .(1/(2(√(a−1)))))/(a−1)) =((πe^(2π(√(a−1))) −(1/(2(√(a−1))))e^(2π(√(a−1))) )/(a−1)) =(((2π(√(a−1))−1)e^(2π(√(a−1))) )/(2(a−1)(√(a−1)))) ⇒ f^′ (a)=−(π/2)(((2π(√(a−1))−1)e^(2π(√(a−1))) )/((a−1)(√(a−1)))) sin(πa) −π^2 cos(πa).(e^(2π(√(a−1))) /( (√(a−1)))) ⇒f^′ (2)=−(π/2)(((2π−1)e^(2π) )/1).0 −π^2 e^(2π) =−π^2 e^(2π) ⇒ ∫_(−∞) ^(+∞) ((sin(πx^2 ))/((x^2 +2x+2)^2 )) =π^2 e^(2π)
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{sin}\left(\pi\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{a}}\mathrm{dx}\:\:\mathrm{with}\:\mathrm{a}>\mathrm{1} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}^{'} \left(\mathrm{a}\right)=−\int_{−\infty} ^{+\infty} \:\frac{\mathrm{sin}\left(\pi\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{a}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{2}\right)=−\int_{−\infty} ^{+\infty} \:\frac{\mathrm{sin}\left(\pi\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{\mathrm{sin}\left(\pi\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}\right)^{\mathrm{2}} }=−\mathrm{f}^{'} \left(\mathrm{2}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{a}\right)=\mathrm{Im}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{i}\pi\mathrm{x}^{\mathrm{2}} } }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{a}}\mathrm{dx}\right)\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\mathrm{i}\pi\mathrm{z}^{\mathrm{2}} } }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{2z}+\mathrm{a}} \\ $$$$\mathrm{poles}\:\mathrm{of}\:\varphi?\:\:\Delta^{'} \:=\mathrm{1}−\mathrm{a}<\mathrm{0}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{a}−\mathrm{1}}\:\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =−\mathrm{1}−\mathrm{i}\sqrt{\mathrm{a}−\mathrm{1}} \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\mathrm{i}\pi\mathrm{z}^{\mathrm{2}} } }{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)}\:\:\mathrm{residus}\:\mathrm{theorem}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{1}} \right)\:=\mathrm{2i}\pi×\frac{\mathrm{e}^{\mathrm{i}\pi\mathrm{z}_{\mathrm{1}} ^{\mathrm{2}} } }{\mathrm{2i}\sqrt{\mathrm{a}−\mathrm{1}}} \\ $$$$=\frac{\pi}{\:\sqrt{\mathrm{a}−\mathrm{1}}}\:\mathrm{e}^{\mathrm{i}\pi\left\{\mathrm{1}−\mathrm{2i}\sqrt{\mathrm{a}−\mathrm{1}}−\mathrm{a}+\mathrm{1}\right)} \:=\frac{\pi}{\:\sqrt{\mathrm{a}−\mathrm{1}}}\:\mathrm{e}^{\mathrm{i}\pi\left\{\mathrm{2}−\mathrm{a}−\mathrm{2i}\sqrt{\mathrm{a}−\mathrm{1}}\right\}} \\ $$$$=\frac{\pi}{\:\sqrt{\mathrm{a}−\mathrm{1}}}\:\mathrm{e}^{\mathrm{i}\pi\left(\mathrm{2}−\mathrm{a}\right)} .\mathrm{e}^{\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}} =\frac{\pi\mathrm{e}^{\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}} }{\:\sqrt{\mathrm{a}−\mathrm{1}}}\left\{\mathrm{cos}\left(\pi\left(\mathrm{2}−\mathrm{a}\right)\right)+\mathrm{isin}\left(\pi\left(\mathrm{2}−\mathrm{a}\right)\right)\right\}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=−\frac{\pi\:\mathrm{e}^{\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}} }{\:\sqrt{\mathrm{a}−\mathrm{1}}}.\mathrm{sin}\left(\pi\mathrm{a}\right)\:\Rightarrow \\ $$$$−\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\pi\left(\frac{\mathrm{e}^{\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}} }{\:\sqrt{\mathrm{a}−\mathrm{1}}}\right)^{,} \mathrm{sin}\left(\pi\mathrm{a}\right)\:+\pi^{\mathrm{2}} \mathrm{cos}\left(\pi\mathrm{a}\right).\frac{\mathrm{e}^{\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}} }{\:\sqrt{\mathrm{a}−\mathrm{1}}}\:\:\mathrm{but} \\ $$$$\left(\frac{\mathrm{e}^{\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}} }{\:\sqrt{\mathrm{a}−\mathrm{1}}}\right)^{'} \:=\frac{\frac{\mathrm{2}\pi}{\mathrm{2}\sqrt{\mathrm{a}−\mathrm{1}}}\mathrm{e}^{\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}} \:.\sqrt{\mathrm{a}−\mathrm{1}}−\mathrm{e}^{\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}} .\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{a}−\mathrm{1}}}}{\mathrm{a}−\mathrm{1}} \\ $$$$=\frac{\pi\mathrm{e}^{\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}} −\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{a}−\mathrm{1}}}\mathrm{e}^{\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}} }{\mathrm{a}−\mathrm{1}}\:=\frac{\left(\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}−\mathrm{1}\right)\mathrm{e}^{\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}} }{\mathrm{2}\left(\mathrm{a}−\mathrm{1}\right)\sqrt{\mathrm{a}−\mathrm{1}}}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=−\frac{\pi}{\mathrm{2}}\frac{\left(\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}−\mathrm{1}\right)\mathrm{e}^{\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}} }{\left(\mathrm{a}−\mathrm{1}\right)\sqrt{\mathrm{a}−\mathrm{1}}}\:\mathrm{sin}\left(\pi\mathrm{a}\right)\:−\pi^{\mathrm{2}} \mathrm{cos}\left(\pi\mathrm{a}\right).\frac{\mathrm{e}^{\mathrm{2}\pi\sqrt{\mathrm{a}−\mathrm{1}}} }{\:\sqrt{\mathrm{a}−\mathrm{1}}} \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\mathrm{2}\right)=−\frac{\pi}{\mathrm{2}}\frac{\left(\mathrm{2}\pi−\mathrm{1}\right)\mathrm{e}^{\mathrm{2}\pi} }{\mathrm{1}}.\mathrm{0}\:\:−\pi^{\mathrm{2}} \:\mathrm{e}^{\mathrm{2}\pi} \:=−\pi^{\mathrm{2}} \:\mathrm{e}^{\mathrm{2}\pi} \:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{\mathrm{sin}\left(\pi\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}\right)^{\mathrm{2}} }\:=\pi^{\mathrm{2}} \:\mathrm{e}^{\mathrm{2}\pi} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *