Question Number 142028 by mnjuly1970 last updated on 25/May/21

$$\:\:\:\:\:\:\:\:…………{Calculus}………\: \\ $$$$\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({sin}\left({x}\right)\right).{e}^{{cos}\left({x}\right)} }{{x}}{dx}=??? \\ $$$$\:…………{m}.{n}….. \\ $$
Answered by mindispower last updated on 25/May/21
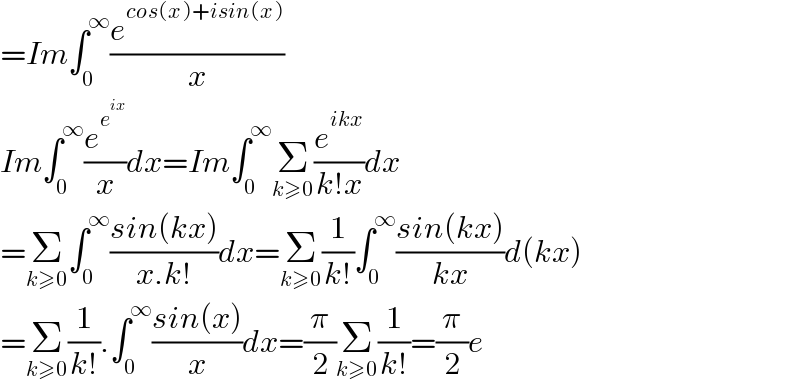
$$={Im}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{cos}\left({x}\right)+{isin}\left({x}\right)} }{{x}} \\ $$$${Im}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{e}^{{ix}} } }{{x}}{dx}={Im}\int_{\mathrm{0}} ^{\infty} \underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{e}^{{ikx}} }{{k}!{x}}{dx} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({kx}\right)}{{x}.{k}!}{dx}=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{k}!}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({kx}\right)}{{kx}}{d}\left({kx}\right) \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{k}!}.\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({x}\right)}{{x}}{dx}=\frac{\pi}{\mathrm{2}}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{k}!}=\frac{\pi}{\mathrm{2}}{e} \\ $$
Commented by mnjuly1970 last updated on 25/May/21

$${zendeh}\:{bashid}\:\:{tashakor}\:.{thanks}\:{alot} \\ $$$${mr}\:{power}\:… \\ $$
Commented by mindispower last updated on 25/May/21
$${withe}\:{pleasur}\:{sir}\:{thank}\:{you} \\ $$
Answered by Dwaipayan Shikari last updated on 25/May/21
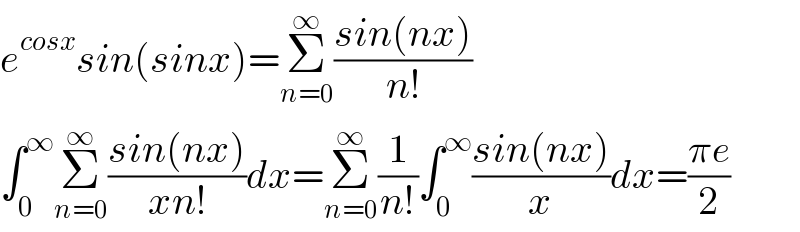
$${e}^{{cosx}} {sin}\left({sinx}\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{sin}\left({nx}\right)}{{n}!} \\ $$$$\int_{\mathrm{0}} ^{\infty} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{sin}\left({nx}\right)}{{xn}!}{dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({nx}\right)}{{x}}{dx}=\frac{\pi{e}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 26/May/21

$$\:\:{thanks}\:{alot}… \\ $$
