calculus-evaluate-k-1-1-k-1-k-2-k-k-1-2-

Question Number 139455 by mnjuly1970 last updated on 27/Apr/21

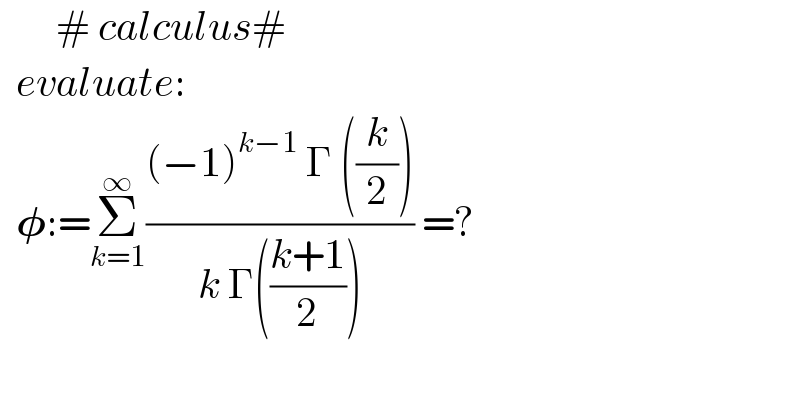
$$\:\:\:\:\:\:\:#\:{calculus}# \\ $$$$\:\:{evaluate}: \\ $$$$\:\:\boldsymbol{\phi}:=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \:\Gamma\:\left(\frac{{k}}{\mathrm{2}}\right)}{{k}\:\Gamma\left(\frac{{k}+\mathrm{1}}{\mathrm{2}}\right)}\:=? \\ $$

Answered by Dwaipayan Shikari last updated on 27/Apr/21

$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} \Gamma\left(\frac{{k}}{\mathrm{2}}\right)}{{k}\Gamma\left(\frac{{k}+\mathrm{1}}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{\:\sqrt{\pi}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} \frac{\mathrm{1}}{{k}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\frac{{k}}{\mathrm{2}}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\pi}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}+\sqrt{{x}}\right)}{{x}\sqrt{\mathrm{1}−{x}}}{dx}=\frac{\mathrm{2}}{\:\sqrt{\pi}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}+{u}\right)}{{u}\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}{du}=\frac{\mathrm{2}}{\:\sqrt{\pi}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{log}\left(\mathrm{1}+{sin}\theta\right)}{{sin}\theta}{d}\theta \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\pi}}\varsigma\left(\mathrm{1}\right) \\ $$$$\varsigma\left({g}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{log}\left(\mathrm{1}+{gsin}\theta\right)}{{sin}\theta}{d}\theta\Rightarrow\varsigma'\left({g}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{1}+{gsin}\theta}{d}\theta \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}{gt}}{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left({t}+{g}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{1}−{g}^{\mathrm{2}} }\right)^{\mathrm{2}} }{dt}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{g}^{\mathrm{2}} }}\left({tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{1}+{g}}{\mathrm{1}−{g}}}−{tan}^{−\mathrm{1}} \frac{{g}}{\:\sqrt{\mathrm{1}−{g}^{\mathrm{2}} }}\right) \\ $$$$\varsigma\left({g}\right)=\mathrm{2}\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{g}^{\mathrm{2}} }}{tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{1}+{g}}{\mathrm{1}−{g}}}\:{dg}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{g}^{\mathrm{2}} }}{tan}^{−\mathrm{1}} \frac{{g}}{\:\sqrt{\mathrm{1}−{g}^{\mathrm{2}} }} \\ $$$$=\mathrm{2}\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{g}^{\mathrm{2}} }}{tan}^{−\mathrm{1}} \frac{\frac{\mathrm{1}+{g}−{g}}{\:\sqrt{\mathrm{1}−{g}^{\mathrm{2}} }}}{\mathrm{1}+\frac{{g}+{g}^{\mathrm{2}} }{\mathrm{1}−{g}^{\mathrm{2}} }}{dg}=\mathrm{2}\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{g}^{\mathrm{2}} }}{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{1}−{g}^{\mathrm{2}} }}{\mathrm{1}+{g}}{dg} \\ $$$${g}={cos}\zeta\:\:\Rightarrow\mathrm{2}\int\frac{−{sin}\zeta}{{sin}\zeta}{tan}^{−\mathrm{1}} \left({tan}\frac{\zeta}{\mathrm{2}}\right){d}\zeta=−\frac{\zeta^{\mathrm{2}} }{\mathrm{2}}+{C}=−\frac{\left({cos}^{−\mathrm{1}} \left({g}\right)\right)^{\mathrm{2}} }{\mathrm{2}}+{C} \\ $$$$\varsigma\left(\mathrm{0}\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{8}}+{C}=\mathrm{0}\Rightarrow{C}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\varsigma\left(\mathrm{1}\right)=−\frac{\mathrm{0}}{\mathrm{2}}+\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$${So}\:\frac{\mathrm{2}}{\:\sqrt{\pi}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{log}\left(\mathrm{1}+{sin}\theta\right)}{{sin}\theta}{d}\theta=\frac{\mathrm{2}}{\:\sqrt{\pi}}.\frac{\pi^{\mathrm{2}} }{\mathrm{8}}=\frac{\pi^{\mathrm{3}/\mathrm{2}} }{\mathrm{4}} \\ $$

Commented by mnjuly1970 last updated on 27/Apr/21

$${thanks}\:{alot}\:{mr}\:{payan}… \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com