Question Number 143508 by mnjuly1970 last updated on 15/Jun/21
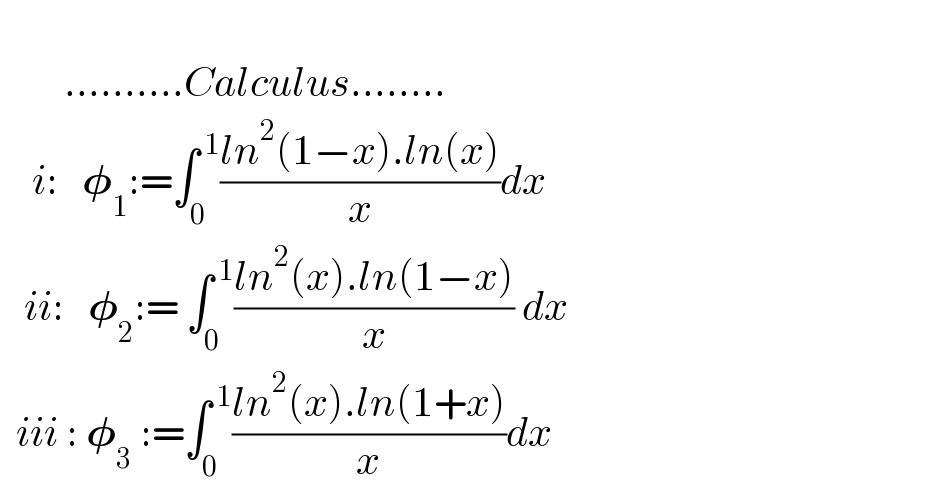
$$ \\ $$$$\:\:\:\:\:\:\:\:……….{Calculus}…….. \\ $$$$\:\:\:\:{i}:\:\:\:\boldsymbol{\phi}_{\mathrm{1}} :=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left(\mathrm{1}β{x}\right).{ln}\left({x}\right)}{{x}}{dx} \\ $$$$\:\:\:{ii}:\:\:\:\boldsymbol{\phi}_{\mathrm{2}} :=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({x}\right).{ln}\left(\mathrm{1}β{x}\right)}{{x}}\:{dx} \\ $$$$\:\:{iii}\::\:\boldsymbol{\phi}_{\mathrm{3}} \::=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({x}\right).{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx} \\ $$
Answered by mindispower last updated on 15/Jun/21
![Ξ¦_1 ,Ξ¦_2 can be found by betta function Ξ¦_1 =(β^3 Ξ²/(β^2 yβx))(0,1)... Ξ¦_3 by part =[((ln^3 (x))/3)ln(1+x)]_0 ^1 β(1/3)β«_0 ^1 ((ln^3 (x))/(1+x))dx =β(1/3)β«_0 ^β ((t^3 e^(βt) )/(1+e^(βt) ))dt=β(1/3)Ξ£_(mβ₯0) β«_0 ^β t^3 (β1)^m e^(β(m+1)t) dt =β(1/3)Ξ£_(mβ₯0) (((β1)^m )/((m+1)^4 ))β«_0 ^β t^3 e^(βt) dt =β(1/3)Ξ£_(mβ₯0) (((β1)^m )/((m+1)^4 ))Ξ(4)=β2Ξ£_(mβ₯0) (1β(1/2^3 ))ΞΆ(4) =β(7/4)ΞΆ(4)](https://www.tinkutara.com/question/Q143511.png)
$$\Phi_{\mathrm{1}} ,\Phi_{\mathrm{2}} \:\:{can}\:{be}\:{found}\:{by}\:{betta}\:{function} \\ $$$$\Phi_{\mathrm{1}} =\frac{\partial^{\mathrm{3}} \beta}{\partial^{\mathrm{2}} {y}\partial{x}}\left(\mathrm{0},\mathrm{1}\right)… \\ $$$$\Phi_{\mathrm{3}} {by}\:{part}\:=\left[\frac{{ln}^{\mathrm{3}} \left({x}\right)}{\mathrm{3}}{ln}\left(\mathrm{1}+{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} β\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{3}} \left({x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$=β\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\mathrm{3}} {e}^{β{t}} }{\mathrm{1}+{e}^{β{t}} }{dt}=β\frac{\mathrm{1}}{\mathrm{3}}\underset{{m}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{3}} \left(β\mathrm{1}\right)^{{m}} {e}^{β\left({m}+\mathrm{1}\right){t}} {dt} \\ $$$$=β\frac{\mathrm{1}}{\mathrm{3}}\underset{{m}\geqslant\mathrm{0}} {\sum}\frac{\left(β\mathrm{1}\right)^{{m}} }{\left({m}+\mathrm{1}\right)^{\mathrm{4}} }\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{3}} {e}^{β{t}} {dt} \\ $$$$=β\frac{\mathrm{1}}{\mathrm{3}}\underset{{m}\geqslant\mathrm{0}} {\sum}\frac{\left(β\mathrm{1}\right)^{{m}} }{\left({m}+\mathrm{1}\right)^{\mathrm{4}} }\Gamma\left(\mathrm{4}\right)=β\mathrm{2}\underset{{m}\geqslant\mathrm{0}} {\sum}\left(\mathrm{1}β\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\right)\zeta\left(\mathrm{4}\right) \\ $$$$=β\frac{\mathrm{7}}{\mathrm{4}}\zeta\left(\mathrm{4}\right) \\ $$
Commented by mnjuly1970 last updated on 15/Jun/21
$$\:{grateful}\:{sir}\:{power} \\ $$
Answered by mathmax by abdo last updated on 15/Jun/21
![Ξ¦_2 =β«_0 ^1 ((log(1βx))/x)log^2 x dx we have log^β² (1βx)=((β1)/(1βx))=βΞ£_(n=0) ^β x^n βlog(1βx)=βΞ£_(n=0) ^β (x^(n+1) /(n+1)) =βΞ£_(n=1) ^β (x^n /n) β((log(1βx))/x)=βΞ£_(n=1) ^β (1/n)x^(nβ1) β Ξ¦_2 =βΞ£_(n=1) ^β (1/n)β«_0 ^1 x^(nβ1) log^2 x dx U_n =β«_0 ^1 x^(nβ1) log^2 x dx βu_n =[(x^n /n)log^2 x]_0 ^1 ββ«_0 ^1 (x^n /n)Γ((2logx)/x)dx =β(2/n)β«_0 ^1 x^(nβ1) logxdx =β(2/n){ [(x^n /n)logx]_0 ^1 ββ«_0 ^1 (x^n /n)(dx/x)} =β(2/n)(β(1/n)β«_0 ^1 x^(nβ1) dx)=(2/n^3 ) βΞ¦_2 =βΞ£_(n=1) ^β (2/n^4 ) =β2ΞΎ(4) =β2Γ(Ο^4 /(90)) =β(Ο^4 /(45))](https://www.tinkutara.com/question/Q143534.png)
$$\Phi_{\mathrm{2}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}\left(\mathrm{1}β\mathrm{x}\right)}{\mathrm{x}}\mathrm{log}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{log}^{'} \left(\mathrm{1}β\mathrm{x}\right)=\frac{β\mathrm{1}}{\mathrm{1}β\mathrm{x}}=β\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:\Rightarrow\mathrm{log}\left(\mathrm{1}β\mathrm{x}\right)=β\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}} \\ $$$$=β\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow\frac{\mathrm{log}\left(\mathrm{1}β\mathrm{x}\right)}{\mathrm{x}}=β\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}}\mathrm{x}^{\mathrm{n}β\mathrm{1}} \:\Rightarrow \\ $$$$\Phi_{\mathrm{2}} =β\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}β\mathrm{1}} \:\mathrm{log}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx} \\ $$$$\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}β\mathrm{1}} \:\mathrm{log}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}\:\Rightarrow\mathrm{u}_{\mathrm{n}} =\left[\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\mathrm{log}^{\mathrm{2}} \mathrm{x}\right]_{\mathrm{0}} ^{\mathrm{1}} β\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}Γ\frac{\mathrm{2logx}}{\mathrm{x}}\mathrm{dx} \\ $$$$=β\frac{\mathrm{2}}{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}β\mathrm{1}} \:\mathrm{logxdx} \\ $$$$=β\frac{\mathrm{2}}{\mathrm{n}}\left\{\:\:\left[\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\mathrm{logx}\right]_{\mathrm{0}} ^{\mathrm{1}} β\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\frac{\mathrm{dx}}{\mathrm{x}}\right\} \\ $$$$=β\frac{\mathrm{2}}{\mathrm{n}}\left(β\frac{\mathrm{1}}{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}β\mathrm{1}} \mathrm{dx}\right)=\frac{\mathrm{2}}{\mathrm{n}^{\mathrm{3}} }\:\Rightarrow\Phi_{\mathrm{2}} =β\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{2}}{\mathrm{n}^{\mathrm{4}} } \\ $$$$=β\mathrm{2}\xi\left(\mathrm{4}\right)\:=β\mathrm{2}Γ\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\:=β\frac{\pi^{\mathrm{4}} }{\mathrm{45}} \\ $$
Commented by mathmax by abdo last updated on 15/Jun/21
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$
Commented by mnjuly1970 last updated on 15/Jun/21
$$\:\:{thanks}\:\:{sir}\:{max} \\ $$
Answered by mathmax by abdo last updated on 15/Jun/21
![Ξ¦_3 =β«_0 ^1 ((log^2 xlog(1+x))/x)dx we have log^β² (1+x)=(1/(1+x))=Ξ£_(n=0) ^β (β1)^n x^n βlog(1+x)=Ξ£_(n=0) ^β (β1)^n (x^(n+1) /(n+1))=Ξ£_(n=1) ^β (((β1)^(nβ1) x^n )/n) β ((log(1+x))/x)=Ξ£_(n=1) ^β (((β1)^(nβ1) )/n)x^(nβ1) βΞ¦_3 =Ξ£_(n=1) ^β (((β1)^(nβ1) )/n)β«_0 ^1 x^(nβ1) log^2 xdx U_n =β«_0 ^1 x^(nβ1) log^2 x dx=[(x^n /n)log^2 x]_0 ^1 ββ«_0 ^1 (x^n /n)Γ((2logx)/x)dx =β(2/n)β«_0 ^1 x^(nβ1) logx dx =β(2/n){[(x^n /n)logx]_0 ^1 ββ«_0 ^1 (x^(nβ1) /n)dx} =(2/n^3 ) βΞ¦_3 =β2Ξ£_(n=1) ^β (((β1)^n )/n^4 )=β2Ξ΄(4) =β2(2^(1β4) β1)ΞΎ(4) =2(1β2^(β3) )ΞΎ(4)=2(1β(1/8))ΞΎ(4) =2Γ(7/8)ΞΎ(4)=(7/4)Γ(Ο^4 /(90)) =((7Ο^4 )/(360))](https://www.tinkutara.com/question/Q143573.png)
$$\Phi_{\mathrm{3}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}^{\mathrm{2}} \mathrm{xlog}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{log}^{'} \left(\mathrm{1}+\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(β\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{log}\left(\mathrm{1}+\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(β\mathrm{1}\right)^{\mathrm{n}} \:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(β\mathrm{1}\right)^{\mathrm{n}β\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow \\ $$$$\frac{\mathrm{log}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(β\mathrm{1}\right)^{\mathrm{n}β\mathrm{1}} }{\mathrm{n}}\mathrm{x}^{\mathrm{n}β\mathrm{1}} \:\Rightarrow\Phi_{\mathrm{3}} =\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \frac{\left(β\mathrm{1}\right)^{\mathrm{n}β\mathrm{1}} }{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}β\mathrm{1}} \:\mathrm{log}^{\mathrm{2}} \mathrm{xdx} \\ $$$$\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}β\mathrm{1}} \mathrm{log}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}=\left[\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\mathrm{log}^{\mathrm{2}} \mathrm{x}\right]_{\mathrm{0}} ^{\mathrm{1}} β\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}Γ\frac{\mathrm{2logx}}{\mathrm{x}}\mathrm{dx} \\ $$$$=β\frac{\mathrm{2}}{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}β\mathrm{1}} \mathrm{logx}\:\mathrm{dx}\:=β\frac{\mathrm{2}}{\mathrm{n}}\left\{\left[\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\mathrm{logx}\right]_{\mathrm{0}} ^{\mathrm{1}} β\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}β\mathrm{1}} }{\mathrm{n}}\mathrm{dx}\right\} \\ $$$$=\frac{\mathrm{2}}{\mathrm{n}^{\mathrm{3}} }\:\Rightarrow\Phi_{\mathrm{3}} =β\mathrm{2}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(β\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{4}} }=β\mathrm{2}\delta\left(\mathrm{4}\right) \\ $$$$=β\mathrm{2}\left(\mathrm{2}^{\mathrm{1}β\mathrm{4}} β\mathrm{1}\right)\xi\left(\mathrm{4}\right)\:=\mathrm{2}\left(\mathrm{1}β\mathrm{2}^{β\mathrm{3}} \right)\xi\left(\mathrm{4}\right)=\mathrm{2}\left(\mathrm{1}β\frac{\mathrm{1}}{\mathrm{8}}\right)\xi\left(\mathrm{4}\right) \\ $$$$=\mathrm{2}Γ\frac{\mathrm{7}}{\mathrm{8}}\xi\left(\mathrm{4}\right)=\frac{\mathrm{7}}{\mathrm{4}}Γ\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\:=\frac{\mathrm{7}\pi^{\mathrm{4}} }{\mathrm{360}} \\ $$