Question Number 135215 by mnjuly1970 last updated on 11/Mar/21
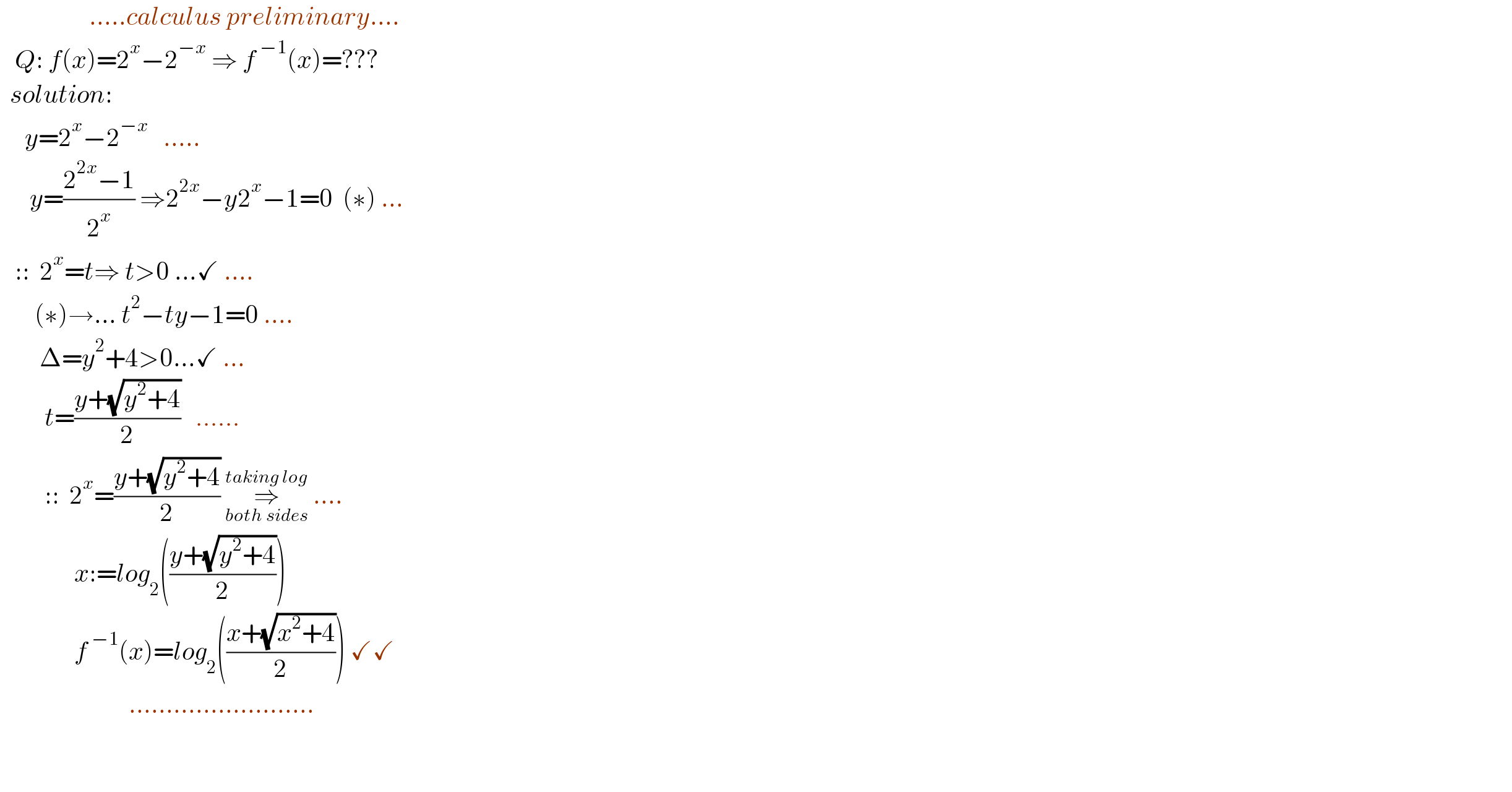
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..{calculus}\:{preliminary}…. \\ $$$$\:\:\:{Q}:\:{f}\left({x}\right)=\mathrm{2}^{{x}} −\mathrm{2}^{−{x}} \:\Rightarrow\:{f}^{\:−\mathrm{1}} \left({x}\right)=??? \\ $$$$\:\:{solution}: \\ $$$$\:\:\:\:\:{y}=\mathrm{2}^{{x}} −\mathrm{2}^{−{x}} \:\:\:….. \\ $$$$\:\:\:\:\:\:{y}=\frac{\mathrm{2}^{\mathrm{2}{x}} −\mathrm{1}}{\mathrm{2}^{{x}} }\:\Rightarrow\mathrm{2}^{\mathrm{2}{x}} −{y}\mathrm{2}^{{x}} −\mathrm{1}=\mathrm{0}\:\:\left(\ast\right)\:… \\ $$$$\:\:\:::\:\:\mathrm{2}^{{x}} ={t}\Rightarrow\:{t}>\mathrm{0}\:…\checkmark\:…. \\ $$$$\:\:\:\:\:\:\:\left(\ast\right)\rightarrow…\:{t}^{\mathrm{2}} −{ty}−\mathrm{1}=\mathrm{0}\:…. \\ $$$$\:\:\:\:\:\:\:\:\Delta={y}^{\mathrm{2}} +\mathrm{4}>\mathrm{0}…\checkmark\:… \\ $$$$\:\:\:\:\:\:\:\:\:{t}=\frac{{y}+\sqrt{{y}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\:\:\:…… \\ $$$$\:\:\:\:\:\:\:\:\:::\:\:\mathrm{2}^{{x}} =\frac{{y}+\sqrt{{y}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\:\underset{{both}\:{sides}} {\overset{{taking}\:{log}} {\Rightarrow}}\:…. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}:={log}_{\mathrm{2}} \left(\frac{{y}+\sqrt{{y}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}^{\:−\mathrm{1}} \left({x}\right)={log}_{\mathrm{2}} \left(\frac{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\right)\:\checkmark\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……………………. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\: \\ $$
