Menu Close

CALCULUS-prove-that-n-1-1-n-1-n-1-2-2n-2log-2-golden-ratio-

Tinku Tara 0 Comments
Pin




Question Number 142970 by mnjuly1970 last updated on 08/Jun/21
..........CALCULUS........... prove that:: 𝛗:=Ξ£_(n=1) ^∞ (((βˆ’1)^(nβˆ’1) ((nβˆ’1)!)^2 )/((2n)!))=2log^2 (Ο•) Ο•=golden ratio.... .............
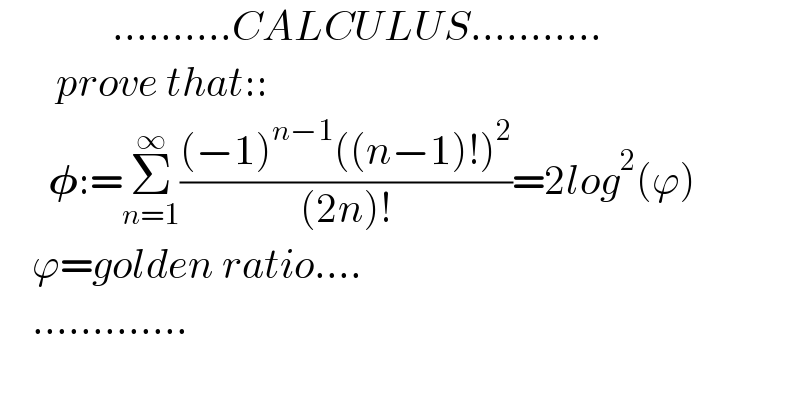
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:……….{CALCULUS}……….. \\ $$$$\:\:\:\:\:\:\:{prove}\:{that}::\:\: \\ $$$$\:\:\:\:\:\:\boldsymbol{\phi}:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(βˆ’\mathrm{1}\right)^{{n}βˆ’\mathrm{1}} \left(\left({n}βˆ’\mathrm{1}\right)!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}\right)!}=\mathrm{2}{log}^{\mathrm{2}} \left(\varphi\right) \\ $$$$\:\:\:\:\varphi={golden}\:{ratio}…. \\ $$$$\:\:\:\:…………. \\ $$
Answered by Dwaipayan Shikari last updated on 08/Jun/21
Ξ£_(n=1) ^∞ ((((nβˆ’1)!)^2 )/((2n)!))(βˆ’1)^(nβˆ’1) =Ξ£_(n=1) ^∞ ((Ξ“(n)Ξ“(n))/(2nΞ“(2n)))(βˆ’1)^(nβˆ’1) =(1/2)∫_0 ^1 Ξ£_(n=1) ^∞ (βˆ’1)^(n+1) (1/n)x^(nβˆ’1) (1βˆ’x)^(nβˆ’1) dx =(1/2)∫_0 ^1 (1/(x(1βˆ’x)))log(1+x(1βˆ’x))dx =(1/2)∫_0 ^1 ((log(1+x(1βˆ’x)))/x)+((log(1+x(1βˆ’x)))/(1βˆ’x)) dx =∫_0 ^1 ((log(1+xβˆ’x^2 ))/x)dx =∫_0 ^1 ((log(x))/(xβˆ’(1/Ο•)))+((log(x))/(x+Ο•))dx=βˆ’(1/Ο•)Ξ£_(n=1) ^∞ ∫_0 ^1 (xΟ•)^n log(x)+(1/Ο•)∫_0 ^1 Ξ£_(n=1) ^∞ (βˆ’xΟ•)^n log(x)dx =(1/Ο•){Ξ£_(n=1) ^∞ (Ο•^n /((n+1)^2 ))+(1/Ο•)Ξ£_(n=1) ^∞ (((βˆ’Ο•)^n )/((n+1)^2 ))} =(1/Ο•^2 )(Li_2 (Ο•)βˆ’Ο•)βˆ’(1/Ο•^2 )(Li_2 (βˆ’Ο•)+Ο•) =(1/Ο•^2 )(Li_2 (Ο•)βˆ’Li_2 (βˆ’Ο•))
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\left({n}βˆ’\mathrm{1}\right)!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}\right)!}\left(βˆ’\mathrm{1}\right)^{{n}βˆ’\mathrm{1}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\Gamma\left({n}\right)\Gamma\left({n}\right)}{\mathrm{2}{n}\Gamma\left(\mathrm{2}{n}\right)}\left(βˆ’\mathrm{1}\right)^{{n}βˆ’\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(βˆ’\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{{n}}{x}^{{n}βˆ’\mathrm{1}} \left(\mathrm{1}βˆ’{x}\right)^{{n}βˆ’\mathrm{1}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}\left(\mathrm{1}βˆ’{x}\right)}{log}\left(\mathrm{1}+{x}\left(\mathrm{1}βˆ’{x}\right)\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}+{x}\left(\mathrm{1}βˆ’{x}\right)\right)}{{x}}+\frac{{log}\left(\mathrm{1}+{x}\left(\mathrm{1}βˆ’{x}\right)\right)}{\mathrm{1}βˆ’{x}}\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}+{x}βˆ’{x}^{\mathrm{2}} \right)}{{x}}{dx}\:\:\:\:\: \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left({x}\right)}{{x}βˆ’\frac{\mathrm{1}}{\varphi}}+\frac{{log}\left({x}\right)}{{x}+\varphi}{dx}=βˆ’\frac{\mathrm{1}}{\varphi}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}\varphi\right)^{{n}} {log}\left({x}\right)+\frac{\mathrm{1}}{\varphi}\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(βˆ’{x}\varphi\right)^{{n}} {log}\left({x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\varphi}\left\{\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\varphi^{{n}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\varphi}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(βˆ’\varphi\right)^{{n}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\right\} \\ $$$$=\frac{\mathrm{1}}{\varphi^{\mathrm{2}} }\left({Li}_{\mathrm{2}} \left(\varphi\right)βˆ’\varphi\right)βˆ’\frac{\mathrm{1}}{\varphi^{\mathrm{2}} }\left({Li}_{\mathrm{2}} \left(βˆ’\varphi\right)+\varphi\right) \\ $$$$=\frac{\mathrm{1}}{\varphi^{\mathrm{2}} }\left({Li}_{\mathrm{2}} \left(\varphi\right)βˆ’{Li}_{\mathrm{2}} \left(βˆ’\varphi\right)\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *