call-lim-n-H-n-ln-n-proof-that-is-finite-and-0-1-

Question Number 2783 by 123456 last updated on 27/Nov/15

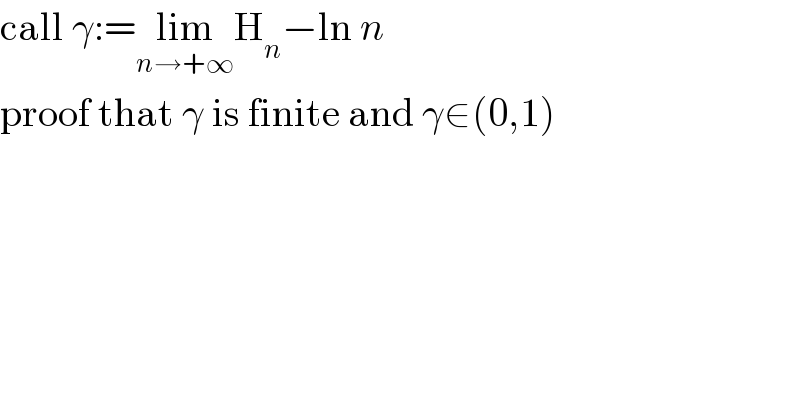
call γ:=lim_(n→+∞) H_n −ln n proof that γ is finite and γ∈(0,1)

$$\mathrm{call}\:\gamma:=\underset{{n}\rightarrow+\infty} {\mathrm{lim}H}_{{n}} −\mathrm{ln}\:{n} \\ $$$$\mathrm{proof}\:\mathrm{that}\:\gamma\:\mathrm{is}\:\mathrm{finite}\:\mathrm{and}\:\gamma\in\left(\mathrm{0},\mathrm{1}\right) \\ $$

Commented by Filup last updated on 27/Nov/15

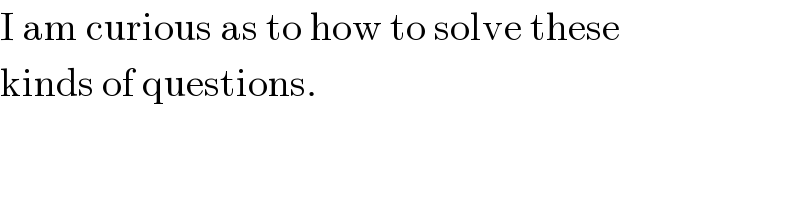
I am curious as to how to solve these kinds of questions.

$$\mathrm{I}\:\mathrm{am}\:\mathrm{curious}\:\mathrm{as}\:\mathrm{to}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{these} \\ $$$$\mathrm{kinds}\:\mathrm{of}\:\mathrm{questions}. \\ $$

Commented by Filup last updated on 27/Nov/15

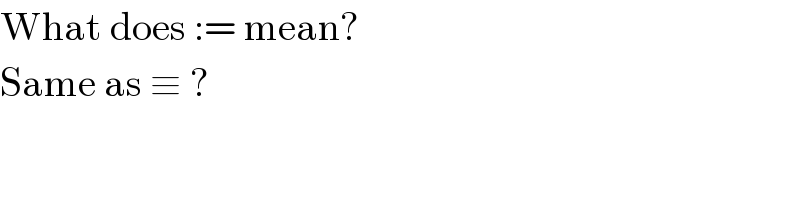
$$\mathrm{What}\:\mathrm{does}\::=\:\mathrm{mean}? \\ $$$$\mathrm{Same}\:\mathrm{as}\:\equiv\:? \\ $$

Commented by 123456 last updated on 27/Nov/15

$$:=\:\mathrm{mean}\:\mathrm{defined} \\ $$$$\mathrm{ex}: \\ $$$${f}\left({x}\right):={x} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$

Commented by Filup last updated on 27/Nov/15

$${Ah}\:\mathrm{I}\:\mathrm{see}! \\ $$

Answered by prakash jain last updated on 27/Nov/15

γ_n =H_n −ln n H_n =1+(1/2)+(1/3)+..+(1/n)=Σ_(i=1) ^n a_i a_i =(1/i) f(x)=(1/x) so that f(i)=a_i Since f(x) is strictly decreasing +ve function. From integral test for series ∫_N ^(M+1) f(x)dx≤Σ_(n=N) ^M f(n)≤f(N)+∫_N ^M f(x)dx ...(A) H_(n−1) ≥∫_1 ^n (1/x)dx=ln n So γ_n =H_n −ln n=(1/n)+H_(n−1) −ln n>0 ...(1) γ_(n+1) =γ_n +(1/(n+1))−ln (n+1)+ln n (1/(n+1))≤ln((n+1)/n) (comparing area of rectangles) ⇒γ_(n+1) =γ_n −[ln ((n+1)/n)−(1/(n+1))]<γ_n γ_n >0 and γ_(n+1) <γ_n So lim_(n→∞) γ_n exists and >0. γ_1 =1−ln 1=1 ∵γ_(n+1) <γ_n 0<γ<1

$$\gamma_{{n}} =\mathrm{H}_{{n}} −\mathrm{ln}\:{n} \\ $$$$\mathrm{H}_{{n}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+..+\frac{\mathrm{1}}{{n}}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} \\ $$$${a}_{{i}} =\frac{\mathrm{1}}{{i}} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{{x}}\:\mathrm{so}\:\mathrm{that}\:{f}\left({i}\right)={a}_{{i}} \\ $$$$\mathrm{Since}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{strictly}\:\mathrm{decreasing}\:+\mathrm{ve}\:\mathrm{function}. \\ $$$$\mathrm{From}\:\mathrm{integral}\:\mathrm{test}\:\mathrm{for}\:\mathrm{series} \\ $$$$\int_{{N}} ^{{M}+\mathrm{1}} {f}\left({x}\right){dx}\leqslant\underset{{n}={N}} {\overset{{M}} {\sum}}\:{f}\left({n}\right)\leqslant{f}\left({N}\right)+\int_{{N}} ^{{M}} {f}\left({x}\right){dx}\:\:…\left({A}\right) \\ $$$$\mathrm{H}_{{n}−\mathrm{1}} \:\geqslant\int_{\mathrm{1}} ^{{n}} \frac{\mathrm{1}}{{x}}{dx}=\mathrm{ln}\:{n} \\ $$$${S}\mathrm{o}\:\gamma_{{n}} =\mathrm{H}_{{n}} −\mathrm{ln}\:{n}=\frac{\mathrm{1}}{{n}}+\mathrm{H}_{{n}−\mathrm{1}} −\mathrm{ln}\:{n}>\mathrm{0}\:\:\:\:\:\:\:…\left(\mathrm{1}\right) \\ $$$$\gamma_{{n}+\mathrm{1}} =\gamma_{{n}} +\frac{\mathrm{1}}{{n}+\mathrm{1}}−\mathrm{ln}\:\left({n}+\mathrm{1}\right)+\mathrm{ln}\:{n} \\ $$$$\frac{\mathrm{1}}{{n}+\mathrm{1}}\leqslant\mathrm{ln}\frac{{n}+\mathrm{1}}{{n}}\:\left({comparing}\:{area}\:{of}\:{rectangles}\right) \\ $$$$\Rightarrow\gamma_{{n}+\mathrm{1}} =\gamma_{{n}} −\left[\mathrm{ln}\:\frac{{n}+\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right]<\gamma_{{n}} \\ $$$$\gamma_{{n}} >\mathrm{0}\:{and}\:\gamma_{{n}+\mathrm{1}} <\gamma_{{n}} \\ $$$$\mathrm{So}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\gamma_{{n}} \:{exists}\:\mathrm{and}\:>\mathrm{0}. \\ $$$$\gamma_{\mathrm{1}} =\mathrm{1}−\mathrm{ln}\:\mathrm{1}=\mathrm{1} \\ $$$$\because\gamma_{{n}+\mathrm{1}} <\gamma_{{n}} \\ $$$$\mathrm{0}<\gamma<\mathrm{1} \\ $$

Commented by RasheedAhmad last updated on 29/Nov/15