Can-you-evaluate-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

Question Number 2286 by Filup last updated on 14/Nov/15

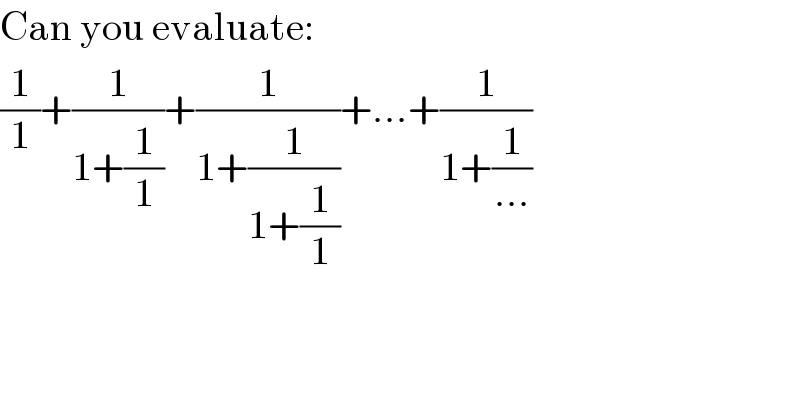
$$\mathrm{Can}\:\mathrm{you}\:\mathrm{evaluate}: \\ $$$$\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}}}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}}}}+…+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{…}} \\ $$

Commented by Yozzi last updated on 14/Nov/15

u_1 =(1/1), u_2 =(1/(1+(1/1)))=(1/(1+u_1 )) u_3 =(1/(1+(1/(1+(1/1)))))=(1/(1+u_2 )) u_4 =(1/(1+(1/(1+(1/(1+(1/1)))))))=(1/(1+u_3 )) Recurrence equation for terms is u_(n+1) =(1/(1+u_n )), u_1 =1,n≥1 u_1 =1 u_2 =(1/(1+u_1 ))=(1/2) u_3 =(1/(1+u_2 ))=(1/(1+(1/2)))=(2/3) u_4 =(1/(1+u_3 ))=(1/(1+(2/3)))=(3/5) u_5 =(1/(1+u_4 ))=(1/(1+(3/5)))=(5/8) u_6 =(1/(1+u_5 ))=(1/(1+(5/8)))=(8/(13))

$${u}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}},\:{u}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}}}=\frac{\mathrm{1}}{\mathrm{1}+{u}_{\mathrm{1}} } \\ $$$${u}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}}}}=\frac{\mathrm{1}}{\mathrm{1}+{u}_{\mathrm{2}} } \\ $$$${u}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}}}}}=\frac{\mathrm{1}}{\mathrm{1}+{u}_{\mathrm{3}} } \\ $$$${Recurrence}\:{equation}\:{for}\:{terms}\:{is} \\ $$$${u}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}+{u}_{{n}} },\:{u}_{\mathrm{1}} =\mathrm{1},{n}\geqslant\mathrm{1} \\ $$$${u}_{\mathrm{1}} =\mathrm{1} \\ $$$${u}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{1}+{u}_{\mathrm{1}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${u}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{1}+{u}_{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${u}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{1}+{u}_{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$${u}_{\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{1}+{u}_{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{5}}}=\frac{\mathrm{5}}{\mathrm{8}} \\ $$$${u}_{\mathrm{6}} =\frac{\mathrm{1}}{\mathrm{1}+{u}_{\mathrm{5}} }=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{5}}{\mathrm{8}}}=\frac{\mathrm{8}}{\mathrm{13}} \\ $$

Commented by Rasheed Soomro last updated on 17/Nov/15

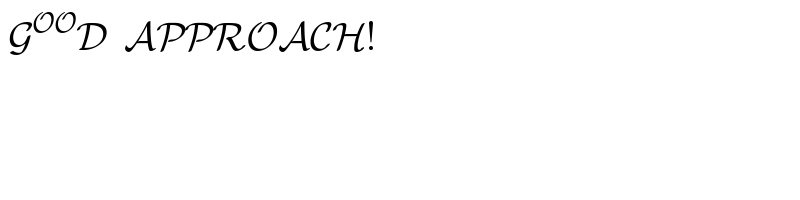
$$\:\mathcal{G}^{\mathcal{OO}} \mathcal{D}\:\:\mathcal{APPROACH}! \\ $$

Commented by prakash jain last updated on 14/Nov/15

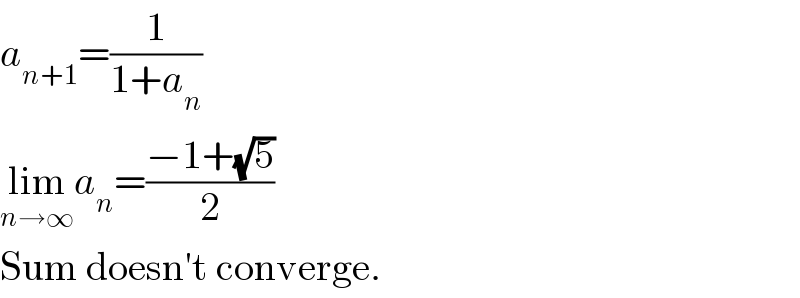
a_(n+1) =(1/(1+a_n )) lim_(n→∞) a_n =((−1+(√5))/2) Sum doesn′t converge.

$${a}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}+{a}_{{n}} } \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}} =\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{Sum}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{converge}. \\ $$

Answered by 123456 last updated on 15/Nov/15

by the coments u_(n+1) =(1/(1+u_n )),u_0 =1 claim 1: u_n =(F_n /F_(n+1) ) F_n are Fibonnaci numbers proof: F_(n+2) =F_(n+1) +F_n for n=1 u_1 =(F_1 /F_2 )=(1/1)=1 (T) suppose its truth for n, lets proof for n+ u_(n+1) =(1/(1+u_n ))=(1/(1+(F_n /F_(n+1) ))) =(1/((F_n +F_(n+1) )/F_(n+1) ))=(F_(n+1) /F_(n+2) ) ■ −−−−−−−−−−−−− S=Σu_n a necesary condition to Σu_n exist is u_n →0 as n→∞ (but not sulficient, 1/n→0 but Σ1/n diverge) but the sum seem to be divergent (F_(n+1) /F_n )→ϕ=((1+(√5))/2) u_n =(F_n /F_(n+1) )=(1/(F_(n+1) /F_n ))→(1/ϕ)=(((√5)−1)/2)

$$\mathrm{by}\:\mathrm{the}\:\mathrm{coments} \\ $$$${u}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}+{u}_{{n}} },{u}_{\mathrm{0}} =\mathrm{1} \\ $$$$\mathrm{claim}\:\mathrm{1}: \\ $$$${u}_{{n}} =\frac{\mathrm{F}_{{n}} }{\mathrm{F}_{{n}+\mathrm{1}} }\:\:\:\:\mathrm{F}_{{n}} \:\mathrm{are}\:\mathrm{Fibonnaci}\:\mathrm{numbers} \\ $$$$\mathrm{proof}: \\ $$$$\mathrm{F}_{{n}+\mathrm{2}} =\mathrm{F}_{{n}+\mathrm{1}} +\mathrm{F}_{{n}} \\ $$$$\mathrm{for}\:{n}=\mathrm{1} \\ $$$${u}_{\mathrm{1}} =\frac{\mathrm{F}_{\mathrm{1}} }{\mathrm{F}_{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{1}}=\mathrm{1}\:\left(\mathrm{T}\right) \\ $$$$\mathrm{suppose}\:\mathrm{its}\:\mathrm{truth}\:\mathrm{for}\:{n},\:\mathrm{lets}\:\mathrm{proof}\:\mathrm{for}\:{n}+ \\ $$$${u}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}+{u}_{{n}} }=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{F}_{{n}} }{\mathrm{F}_{{n}+\mathrm{1}} }} \\ $$$$=\frac{\mathrm{1}}{\frac{\mathrm{F}_{{n}} +\mathrm{F}_{{n}+\mathrm{1}} }{\mathrm{F}_{{n}+\mathrm{1}} }}=\frac{\mathrm{F}_{{n}+\mathrm{1}} }{\mathrm{F}_{{n}+\mathrm{2}} }\:\:\blacksquare \\ $$$$−−−−−−−−−−−−− \\ $$$$\mathrm{S}=\Sigma{u}_{{n}} \\ $$$$\mathrm{a}\:\mathrm{necesary}\:\mathrm{condition}\:\mathrm{to}\:\Sigma{u}_{{n}} \:\mathrm{exist}\:\mathrm{is} \\ $$$${u}_{{n}} \rightarrow\mathrm{0}\:\mathrm{as}\:{n}\rightarrow\infty\:\left(\mathrm{but}\:\mathrm{not}\:\mathrm{sulficient},\:\mathrm{1}/{n}\rightarrow\mathrm{0}\:\mathrm{but}\:\Sigma\mathrm{1}/{n}\:\mathrm{diverge}\right) \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{seem}\:\mathrm{to}\:\mathrm{be}\:\mathrm{divergent} \\ $$$$\frac{\mathrm{F}_{{n}+\mathrm{1}} }{\mathrm{F}_{{n}} }\rightarrow\varphi=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${u}_{{n}} =\frac{\mathrm{F}_{{n}} }{\mathrm{F}_{{n}+\mathrm{1}} }=\frac{\mathrm{1}}{\frac{\mathrm{F}_{{n}+\mathrm{1}} }{\mathrm{F}_{{n}} }}\rightarrow\frac{\mathrm{1}}{\varphi}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}} \\ $$

Commented by prakash jain last updated on 15/Nov/15

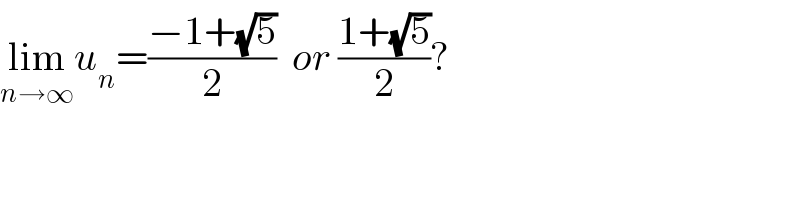
lim_(n→∞) u_n =((−1+(√5))/2) or ((1+(√5))/2)?

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{u}_{{n}} =\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\:{or}\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}? \\ $$

Commented by 123456 last updated on 15/Nov/15

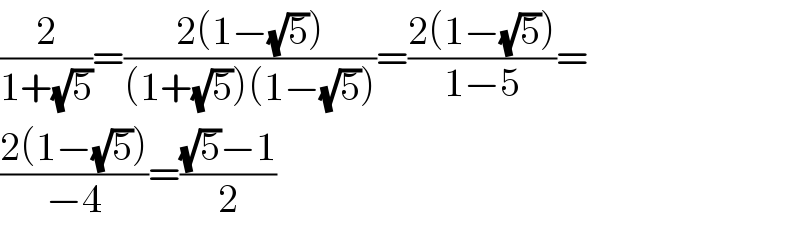
(2/(1+(√5)))=((2(1−(√5)))/((1+(√5))(1−(√5))))=((2(1−(√5)))/(1−5))= ((2(1−(√5)))/(−4))=(((√5)−1)/2)

$$\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{5}}}=\frac{\mathrm{2}\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)}{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)}=\frac{\mathrm{2}\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)}{\mathrm{1}−\mathrm{5}}= \\ $$$$\frac{\mathrm{2}\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)}{−\mathrm{4}}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}} \\ $$

Facebook Tweet Pin

Can-you-evaluate-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-

Leave a Reply Cancel reply