Question Number 6028 by FilupSmith last updated on 10/Jun/16

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{show}\:\mathrm{me}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve}: \\ $$$${L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}^{{n}} }{{n}!} \\ $$
Commented by Yozzii last updated on 10/Jun/16
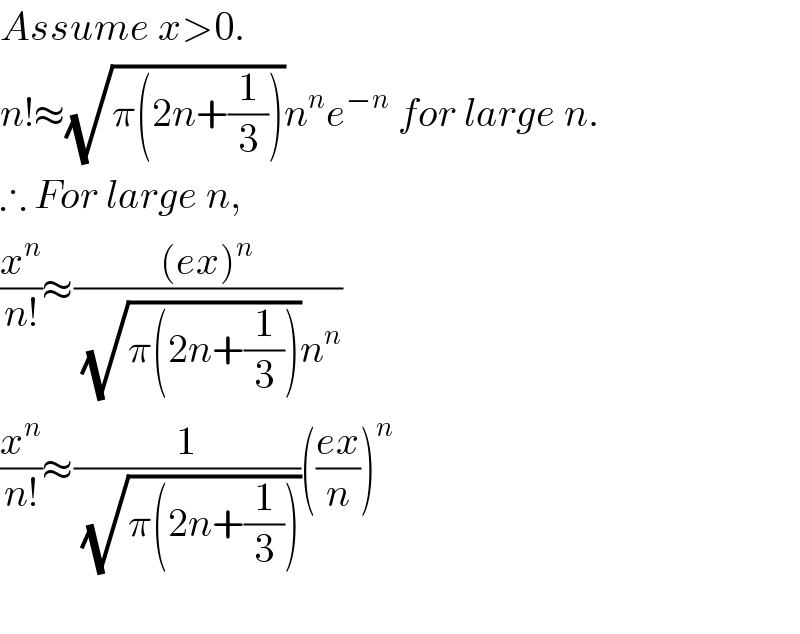
$${Assume}\:{x}>\mathrm{0}. \\ $$$${n}!\approx\sqrt{\pi\left(\mathrm{2}{n}+\frac{\mathrm{1}}{\mathrm{3}}\right)}{n}^{{n}} {e}^{−{n}} \:{for}\:{large}\:{n}. \\ $$$$\therefore\:{For}\:{large}\:{n},\: \\ $$$$\frac{{x}^{{n}} }{{n}!}\approx\frac{\left({ex}\right)^{{n}} }{\:\sqrt{\pi\left(\mathrm{2}{n}+\frac{\mathrm{1}}{\mathrm{3}}\right)}{n}^{{n}} } \\ $$$$\frac{{x}^{{n}} }{{n}!}\approx\frac{\mathrm{1}}{\:\sqrt{\pi\left(\mathrm{2}{n}+\frac{\mathrm{1}}{\mathrm{3}}\right)}}\left(\frac{{ex}}{{n}}\right)^{{n}} \\ $$$$ \\ $$
Commented by Yozzii last updated on 10/Jun/16
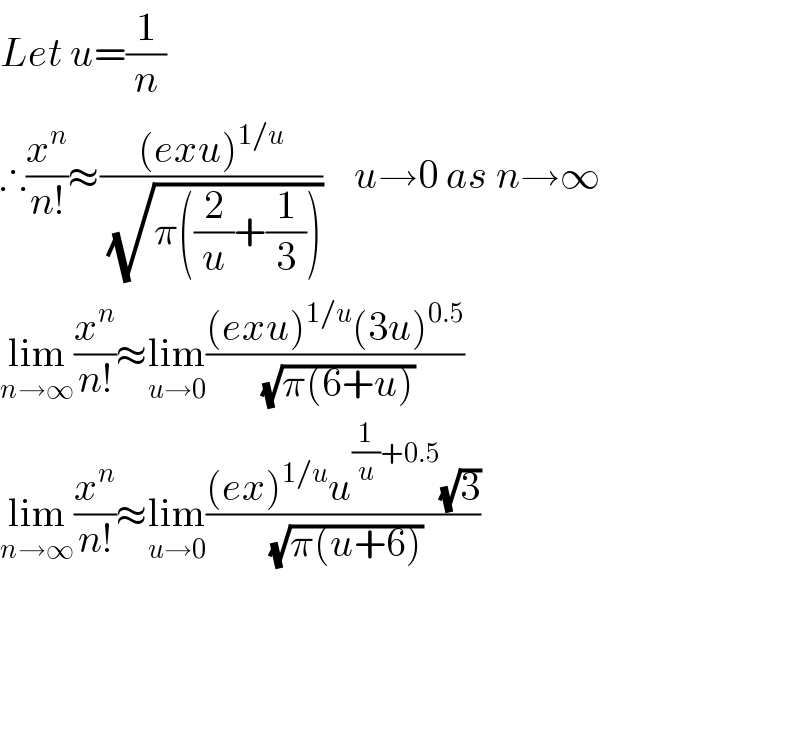
$${Let}\:{u}=\frac{\mathrm{1}}{{n}} \\ $$$$\therefore\frac{{x}^{{n}} }{{n}!}\approx\frac{\left({exu}\right)^{\mathrm{1}/{u}} }{\:\sqrt{\pi\left(\frac{\mathrm{2}}{{u}}+\frac{\mathrm{1}}{\mathrm{3}}\right)}}\:\:\:\:{u}\rightarrow\mathrm{0}\:{as}\:{n}\rightarrow\infty \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{x}^{{n}} }{{n}!}\approx\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({exu}\right)^{\mathrm{1}/{u}} \left(\mathrm{3}{u}\right)^{\mathrm{0}.\mathrm{5}} }{\:\sqrt{\pi\left(\mathrm{6}+{u}\right)}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{x}^{{n}} }{{n}!}\approx\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({ex}\right)^{\mathrm{1}/{u}} {u}^{\frac{\mathrm{1}}{{u}}+\mathrm{0}.\mathrm{5}} \sqrt{\mathrm{3}}}{\:\sqrt{\pi\left({u}+\mathrm{6}\right)}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
