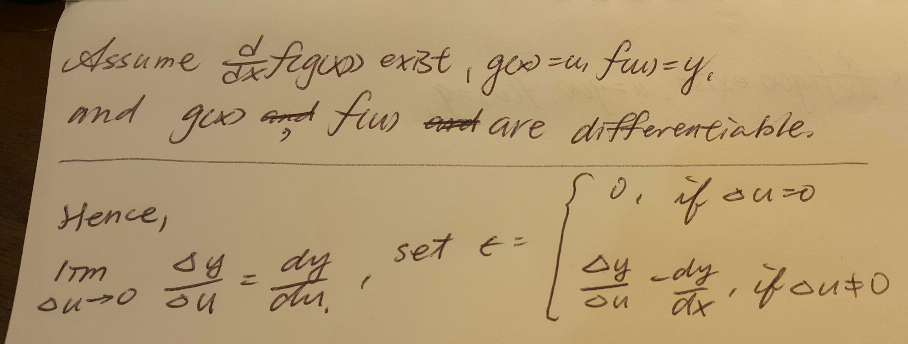Question Number 11581 by Nayon last updated on 28/Mar/17
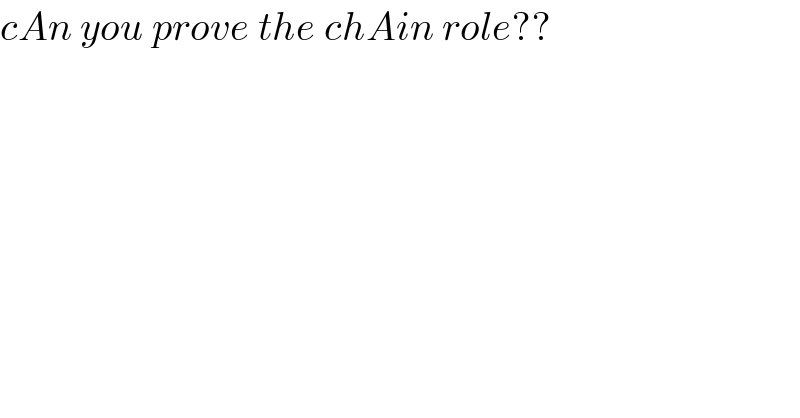
$${cAn}\:{you}\:{prove}\:{the}\:{chAin}\:{role}?? \\ $$
Answered by linkelly0615 last updated on 28/Mar/17

$${yes}\sim \\ $$
Commented by linkelly0615 last updated on 28/Mar/17

$$\left({BELOW}\right) \\ $$
Answered by linkelly0615 last updated on 28/Mar/17
![set that [f(g(x))]′ exist [f(g(x))]′=lim_(h→0) (([f(g(x+h))]−[f(g(x))])/h) ∵g(x+h)=g(x)+hg′(x)+(h^2 /2)g′′(x)+...... ∴when “h” is small enough then g(x+h)≈g(x)+hg′(x) ⇒[f(g(x+h))]≈[f(g(x)+hg′(x))] if “hg′(x)” is small enough then [f(g(x)+hg′(x))]≈[f(g(x))+(hg′(x))f′(g(x))] ... ⇒ [f(g(x))]′=lim_(h→0) (([f(g(x+h))]−[f(g(x))])/h) =lim_(h→0) (([f(g(x)+hg′(x))]−[f(g(x))])/h) =lim_(h→0) (([f(g(x))+(hg′(x))f′(g(x))]−[f(g(x))])/h) =f′(g(x))g′(x)](https://www.tinkutara.com/question/Q11583.png)
$$ \\ $$$${set}\:{that}\:\left[{f}\left({g}\left({x}\right)\right)\right]'\:{exist} \\ $$$$ \\ $$$$\left[{f}\left({g}\left({x}\right)\right)\right]'=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left[{f}\left({g}\left({x}+{h}\right)\right)\right]−\left[{f}\left({g}\left({x}\right)\right)\right]}{{h}} \\ $$$$\because{g}\left({x}+{h}\right)={g}\left({x}\right)+{hg}'\left({x}\right)+\frac{{h}^{\mathrm{2}} }{\mathrm{2}}{g}''\left({x}\right)+…… \\ $$$$\therefore{when}\:“{h}''\:{is}\:{small}\:{enough} \\ $$$${then} \\ $$$${g}\left({x}+{h}\right)\approx{g}\left({x}\right)+{hg}'\left({x}\right) \\ $$$$\Rightarrow\left[{f}\left({g}\left({x}+{h}\right)\right)\right]\approx\left[{f}\left({g}\left({x}\right)+{hg}'\left({x}\right)\right)\right] \\ $$$${if}\:“{hg}'\left({x}\right)''\:{is}\:{small}\:{enough} \\ $$$${then} \\ $$$$\left[{f}\left({g}\left({x}\right)+{hg}'\left({x}\right)\right)\right]\approx\left[{f}\left({g}\left({x}\right)\right)+\left({hg}'\left({x}\right)\right){f}'\left({g}\left({x}\right)\right)\right] \\ $$$$… \\ $$$$\Rightarrow \\ $$$$\left[{f}\left({g}\left({x}\right)\right)\right]'=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left[{f}\left({g}\left({x}+{h}\right)\right)\right]−\left[{f}\left({g}\left({x}\right)\right)\right]}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left[{f}\left({g}\left({x}\right)+{hg}'\left({x}\right)\right)\right]−\left[{f}\left({g}\left({x}\right)\right)\right]}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left[{f}\left({g}\left({x}\right)\right)+\left({hg}'\left({x}\right)\right){f}'\left({g}\left({x}\right)\right)\right]−\left[{f}\left({g}\left({x}\right)\right)\right]}{{h}} \\ $$$$={f}'\left({g}\left({x}\right)\right){g}'\left({x}\right)\:\: \\ $$
Commented by linkelly0615 last updated on 28/Mar/17
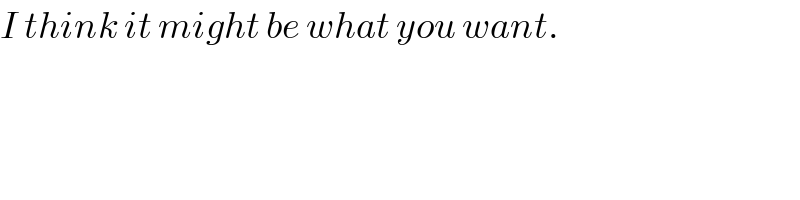
$${I}\:{think}\:{it}\:{might}\:{be}\:{what}\:{you}\:{want}. \\ $$
Commented by Nayon last updated on 29/Mar/17
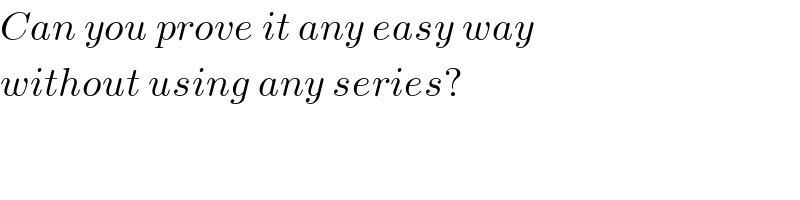
$${Can}\:{you}\:{prove}\:{it}\:{any}\:{easy}\:{way}\: \\ $$$${without}\:{using}\:{any}\:{series}? \\ $$
Commented by linkelly0615 last updated on 29/Mar/17

Commented by linkelly0615 last updated on 29/Mar/17

$${Maybe}\:{it}\:{is}\:{okay} \\ $$$${if}\:{not}\:…{I}\:{will}\:{try}… \\ $$$$\mathrm{actually},\:{I}\:{am}\:{trying}\:{to}\:{find}\: \\ $$$${some}\:{diffrent}\:{ways}\:{to}\:{prove}\: \\ $$$${that}\:{rule}\:… \\ $$$$\left({Including}\:{a}\:{crazy}\:{way}\right) \\ $$$$ \\ $$
Commented by Nayon last updated on 29/Mar/17
$${it}\:{is}\:{not}\:{seen}\:{properlly}….\:{please} \\ $$$${comment}\:{a}\:{clear}\:{one}.. \\ $$
Commented by linkelly0615 last updated on 29/Mar/17
$${it}\:{can}\:{zoom}\:{in}\:{by}\:{your}\:{finger}… \\ $$$$ \\ $$
Commented by linkelly0615 last updated on 29/Mar/17