Menu Close

Can-you-show-why-a-d-dx-sin-x-cos-x-b-d-dx-cos-x-sin-x-

Tinku Tara 0 Comments
Pin




Question Number 5171 by FilupSmith last updated on 25/Apr/16
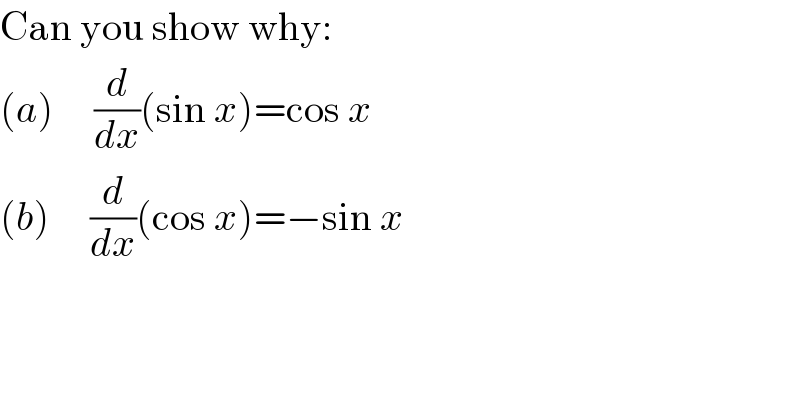
Can you show why: (a) (d/dx)(sin x)=cos x (b) (d/dx)(cos x)=−sin x
$$\mathrm{Can}\:\mathrm{you}\:\mathrm{show}\:\mathrm{why}: \\ $$$$\left({a}\right)\:\:\:\:\:\frac{{d}}{{dx}}\left(\mathrm{sin}\:{x}\right)=\mathrm{cos}\:{x} \\ $$$$\left({b}\right)\:\:\:\:\:\frac{{d}}{{dx}}\left(\mathrm{cos}\:{x}\right)=−\mathrm{sin}\:{x} \\ $$
Commented by FilupSmith last updated on 25/Apr/16
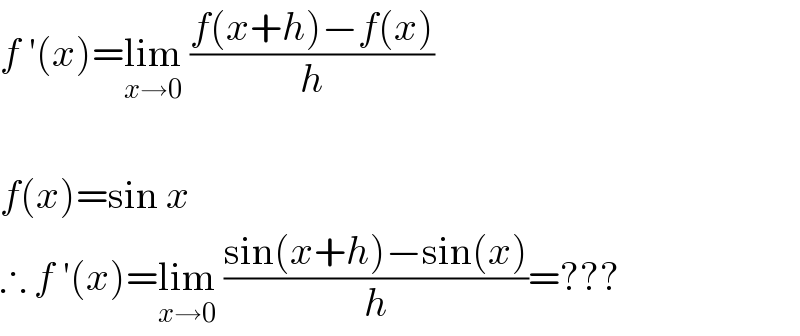
f ′(x)=lim_(x→0) ((f(x+h)−f(x))/h) f(x)=sin x ∴ f ′(x)=lim_(x→0) ((sin(x+h)−sin(x))/h)=???
$${f}\:'\left({x}\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{f}\left({x}+{h}\right)−{f}\left({x}\right)}{{h}} \\ $$$$ \\ $$$${f}\left({x}\right)=\mathrm{sin}\:{x} \\ $$$$\therefore\:{f}\:'\left({x}\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\left({x}+{h}\right)−\mathrm{sin}\left({x}\right)}{{h}}=??? \\ $$
Answered by 123456 last updated on 25/Apr/16
f′(x)=lim_(h→0) ((f(x+h)−f(x))/h) f(x)=sin x f′(x)=lim_(h→0) ((sin (x+h)−sin x)/h) =lim_(h→0) ((sin hcos x+sin xcos h−sin x)/h) =cos xlim_(h→0) ((sin h)/h)+sin xlim_(h→0) ((1−cos h)/h) =cos x f(x)=cos x f′(x)=lim_(h→0) ((cos (x+h)−cos x)/h) =lim_(h→0) ((cos xcos h−sin xsin h−cos x)/h) =−cos xlim_(h→0) ((1−cos h)/h)−sin xlim_(h→0) ((sin h)/h) =−sin x where we used sum of trigonometric function sin (α+β)=sin αcos β+cos αsin β cos (α+β)=cos αcos β−sin αsin β fundamental limit lim_(h→0) ((sin h)/h)=1 lim_(h→0) ((1−cos h)/h)=0
$${f}'\left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left({x}+{h}\right)−{f}\left({x}\right)}{{h}} \\ $$$${f}\left({x}\right)=\mathrm{sin}\:{x} \\ $$$${f}'\left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left({x}+{h}\right)−\mathrm{sin}\:{x}}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{h}\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\mathrm{cos}\:{h}−\mathrm{sin}\:{x}}{{h}} \\ $$$$=\mathrm{cos}\:{x}\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{h}}{{h}}+\mathrm{sin}\:{x}\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:{h}}{{h}} \\ $$$$=\mathrm{cos}\:{x} \\ $$$${f}\left({x}\right)=\mathrm{cos}\:{x} \\ $$$${f}'\left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:\left({x}+{h}\right)−\mathrm{cos}\:{x}}{{h}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:{x}\mathrm{cos}\:{h}−\mathrm{sin}\:{x}\mathrm{sin}\:{h}−\mathrm{cos}\:{x}}{{h}} \\ $$$$=−\mathrm{cos}\:{x}\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:{h}}{{h}}−\mathrm{sin}\:{x}\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{h}}{{h}} \\ $$$$=−\mathrm{sin}\:{x} \\ $$$$\mathrm{where}\:\mathrm{we}\:\mathrm{used} \\ $$$$\mathrm{sum}\:\mathrm{of}\:\mathrm{trigonometric}\:\mathrm{function} \\ $$$$\mathrm{sin}\:\left(\alpha+\beta\right)=\mathrm{sin}\:\alpha\mathrm{cos}\:\beta+\mathrm{cos}\:\alpha\mathrm{sin}\:\beta \\ $$$$\mathrm{cos}\:\left(\alpha+\beta\right)=\mathrm{cos}\:\alpha\mathrm{cos}\:\beta−\mathrm{sin}\:\alpha\mathrm{sin}\:\beta \\ $$$$\mathrm{fundamental}\:\mathrm{limit} \\ $$$$\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{h}}{\mathrm{h}}=\mathrm{1} \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:{h}}{{h}}=\mathrm{0} \\ $$
Commented by FilupSmith last updated on 25/Apr/16
ahh i see thank you
$${ahh}\:{i}\:{see}\:{thank}\:{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *