Question Number 6042 by FilupSmith last updated on 10/Jun/16

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{indefinite}\:\mathrm{integral}: \\ $$$$\int{e}^{−{u}} {u}^{{n}} {du} \\ $$
Commented by Yozzii last updated on 11/Jun/16
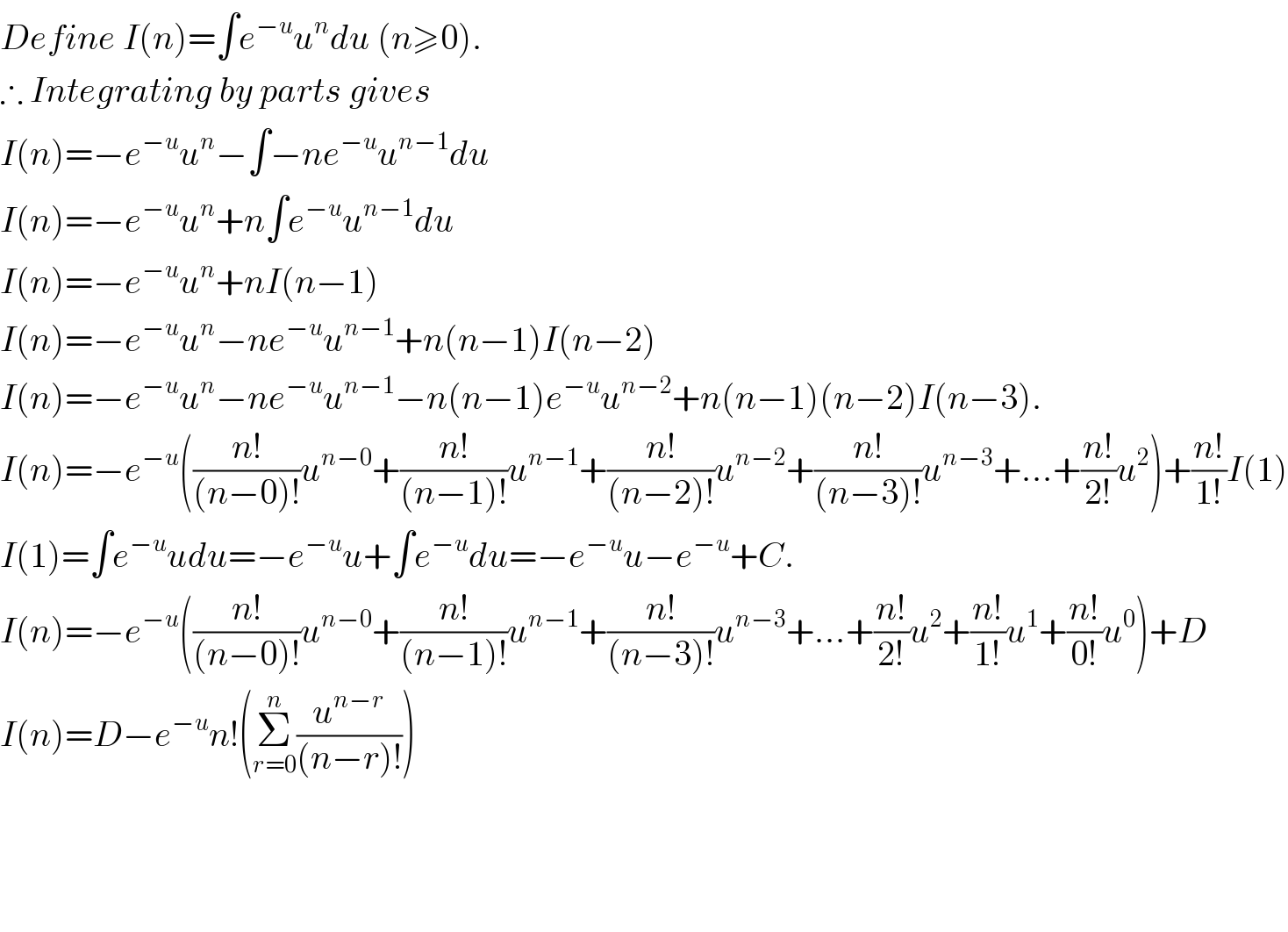
$${Define}\:{I}\left({n}\right)=\int{e}^{−{u}} {u}^{{n}} {du}\:\left({n}\geqslant\mathrm{0}\right). \\ $$$$\therefore\:{Integrating}\:{by}\:{parts}\:{gives} \\ $$$${I}\left({n}\right)=−{e}^{−{u}} {u}^{{n}} −\int−{ne}^{−{u}} {u}^{{n}−\mathrm{1}} {du} \\ $$$${I}\left({n}\right)=−{e}^{−{u}} {u}^{{n}} +{n}\int{e}^{−{u}} {u}^{{n}−\mathrm{1}} {du} \\ $$$${I}\left({n}\right)=−{e}^{−{u}} {u}^{{n}} +{nI}\left({n}−\mathrm{1}\right) \\ $$$${I}\left({n}\right)=−{e}^{−{u}} {u}^{{n}} −{ne}^{−{u}} {u}^{{n}−\mathrm{1}} +{n}\left({n}−\mathrm{1}\right){I}\left({n}−\mathrm{2}\right) \\ $$$${I}\left({n}\right)=−{e}^{−{u}} {u}^{{n}} −{ne}^{−{u}} {u}^{{n}−\mathrm{1}} −{n}\left({n}−\mathrm{1}\right){e}^{−{u}} {u}^{{n}−\mathrm{2}} +{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right){I}\left({n}−\mathrm{3}\right). \\ $$$${I}\left({n}\right)=−{e}^{−{u}} \left(\frac{{n}!}{\left({n}−\mathrm{0}\right)!}{u}^{{n}−\mathrm{0}} +\frac{{n}!}{\left({n}−\mathrm{1}\right)!}{u}^{{n}−\mathrm{1}} +\frac{{n}!}{\left({n}−\mathrm{2}\right)!}{u}^{{n}−\mathrm{2}} +\frac{{n}!}{\left({n}−\mathrm{3}\right)!}{u}^{{n}−\mathrm{3}} +…+\frac{{n}!}{\mathrm{2}!}{u}^{\mathrm{2}} \right)+\frac{{n}!}{\mathrm{1}!}{I}\left(\mathrm{1}\right) \\ $$$${I}\left(\mathrm{1}\right)=\int{e}^{−{u}} {udu}=−{e}^{−{u}} {u}+\int{e}^{−{u}} {du}=−{e}^{−{u}} {u}−{e}^{−{u}} +{C}. \\ $$$${I}\left({n}\right)=−{e}^{−{u}} \left(\frac{{n}!}{\left({n}−\mathrm{0}\right)!}{u}^{{n}−\mathrm{0}} +\frac{{n}!}{\left({n}−\mathrm{1}\right)!}{u}^{{n}−\mathrm{1}} +\frac{{n}!}{\left({n}−\mathrm{3}\right)!}{u}^{{n}−\mathrm{3}} +…+\frac{{n}!}{\mathrm{2}!}{u}^{\mathrm{2}} +\frac{{n}!}{\mathrm{1}!}{u}^{\mathrm{1}} +\frac{{n}!}{\mathrm{0}!}{u}^{\mathrm{0}} \right)+{D} \\ $$$${I}\left({n}\right)={D}−{e}^{−{u}} {n}!\left(\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{u}^{{n}−{r}} }{\left({n}−{r}\right)!}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by FilupSmith last updated on 11/Jun/16

$$\mathrm{is}\:\mathrm{a}\:{D}\:\mathrm{constant}? \\ $$
Commented by Yozzii last updated on 11/Jun/16
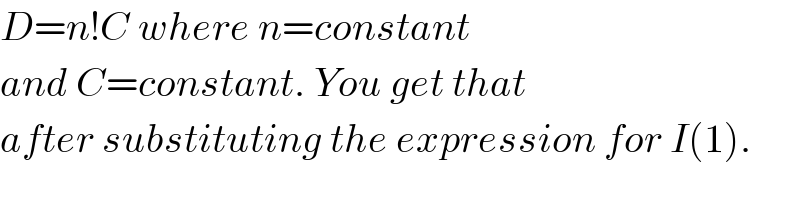
$${D}={n}!{C}\:{where}\:{n}={constant} \\ $$$${and}\:{C}={constant}.\:{You}\:{get}\:{that} \\ $$$${after}\:{substituting}\:{the}\:{expression}\:{for}\:{I}\left(\mathrm{1}\right). \\ $$$$ \\ $$
Commented by FilupSmith last updated on 11/Jun/16

$$\mathrm{I}\:\mathrm{see},\:\mathrm{thank}\:\mathrm{you}! \\ $$
