Question Number 135490 by benjo_mathlover last updated on 13/Mar/21

$${Combination} \\ $$A committee of 8 people is to be formed from 7 women and 5 men. In how many ways can the members be chosen so as to include at least 3 men?
Answered by EDWIN88 last updated on 13/Mar/21
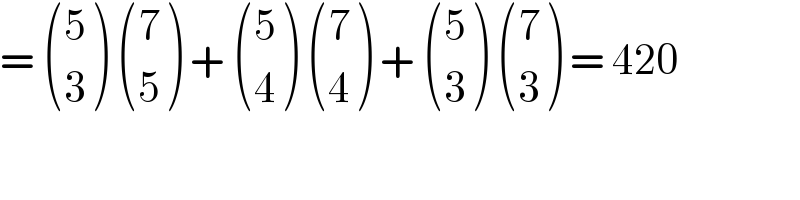
$$=\:\begin{pmatrix}{\mathrm{5}}\\{\mathrm{3}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{7}}\\{\mathrm{5}}\end{pmatrix}\:+\:\begin{pmatrix}{\mathrm{5}}\\{\mathrm{4}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{7}}\\{\mathrm{4}}\end{pmatrix}\:+\:\begin{pmatrix}{\mathrm{5}}\\{\mathrm{3}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{7}}\\{\mathrm{3}}\end{pmatrix}\:=\:\mathrm{420} \\ $$
Answered by mr W last updated on 13/Mar/21

$${the}\:{coef}.\:{of}\:{term}\:{x}^{\mathrm{8}} \:{in} \\ $$$$\left({C}_{\mathrm{3}} ^{\mathrm{5}} {x}^{\mathrm{3}} +{C}_{\mathrm{4}} ^{\mathrm{5}} {x}^{\mathrm{4}} +{C}_{\mathrm{5}} ^{\mathrm{5}} {x}^{\mathrm{5}} \right)\left(\mathrm{1}+{C}_{\mathrm{1}} ^{\mathrm{7}} {x}+{C}_{\mathrm{2}} ^{\mathrm{7}} {x}^{\mathrm{2}} +…+{C}_{\mathrm{7}} ^{\mathrm{7}} {x}^{\mathrm{7}} \right) \\ $$$${is}\:\mathrm{420}.\:{that}\:{means}\:{there}\:{are}\:\mathrm{420}\:{ways}. \\ $$
Commented by mr W last updated on 13/Mar/21

Answered by physicstutes last updated on 13/Mar/21

$$\mathrm{i}\:\mathrm{like}\:\mathrm{looking}\:\mathrm{at}\:\mathrm{it}\:\mathrm{from}\:\mathrm{this}\:\mathrm{pespective}.\:\mathrm{see}\:\mathrm{the}\:\mathrm{table}\:\mathrm{below} \\ $$$$\mathrm{which}\:\mathrm{shows}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{men}\:\mathrm{and}\:\mathrm{women}\:\mathrm{selected}\:\mathrm{based}\:\mathrm{on} \\ $$$$\mathrm{the}\:\mathrm{above}\:\mathrm{conditions} \\ $$$$\:\begin{array}{|c|c|c|c|}{\mathrm{number}\:\mathrm{of}\:\mathrm{men}}&\hline{\mathrm{number}\:\mathrm{of}\:\mathrm{women}}\\{\mathrm{3}}&\hline{\mathrm{5}}\\{\mathrm{4}}&\hline{\mathrm{4}}\\{\mathrm{5}}&\hline{\mathrm{3}}\\\hline\end{array} \\ $$$$\:\mathrm{therefore}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{ways}\:=\:^{\mathrm{5}} {C}_{\mathrm{3}} ×^{\mathrm{8}} {C}_{\mathrm{5}} \:+\:^{\mathrm{5}} {C}_{\mathrm{4}} ×^{\mathrm{8}} {C}_{\mathrm{4}} \:+\:^{\mathrm{5}} {C}_{\mathrm{5}} ×^{\mathrm{5}} {C}_{\mathrm{3}} \:=\:\mathrm{420}\:\mathrm{ways} \\ $$
Commented by mr W last updated on 13/Mar/21

$${in}\:{this}\:{case}\:{you}\:{can}\:{use}\:{this}\:{method}. \\ $$$${but}\:{for}\:{complex}\:{cases}\:{for}\:{example} \\ $$$${there}\:{are}\:\mathrm{10}\:{men},\:\mathrm{12}\:{women},\:\mathrm{8}\:{boys}, \\ $$$$\mathrm{7}\:{girls}.\:{a}\:{committee}\:{with}\:\mathrm{10}\:{persons} \\ $$$${should}\:{be}\:{formed},\:{we}\:{need}\:{other} \\ $$$${methods}. \\ $$
Commented by physicstutes last updated on 13/Mar/21

$$\mathrm{sure}\:\mathrm{sir}\:\mathrm{i}\:\mathrm{totally}\:\mathrm{know}\:\mathrm{that}. \\ $$
