Compute-lim-A-1-A-1-A-A-1-x-dx-IMC-2015-

Question Number 7501 by Yozzia last updated on 01/Sep/16

C o m p u t e \lim_{A \to + \infty} {\frac{1}{A} \int_{1}^{A} A^{\frac{1}{x}} d x} .

(I M C 2015)

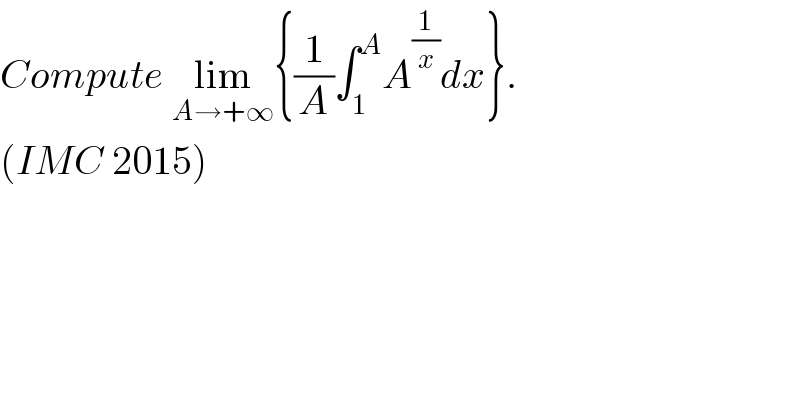
Answered by FilupSmith last updated on 01/Sep/16

L = \lim_{A \to \infty} {\frac{1}{A} \int_{1}^{A} A^{\frac{1}{x}} d x}

u n s u r e i f m a t h i s c o r r e c t .

L = \lim_{A \to \infty} {\frac{1}{A} \int_{1}^{A} e^{\frac{1}{x} \ln (A)} d x}

u = e^{\frac{1}{x} \ln (A)} \Rightarrow d u = - x^{- 2} \ln (A) e^{x^{- 1} \ln (A)} d x

x = \frac{\ln (A)}{\ln (u)}

d u = - \frac{\ln (u)}{x} u d x

d u = - \frac{\ln^{2} (u)}{\ln (A)} u d x

d x = - \frac{\ln (A)}{u \ln^{2} (u)} d u

L = \lim_{A \to \infty} {\frac{1}{A} \int_{x = 1}^{x = A} u (- \frac{\ln (A)}{u \ln^{2} (u)} d u)}

L = \lim_{A \to \infty} {- \frac{1}{A} \int_{x = 1}^{x = A} u \frac{\ln (A)}{u \ln^{2} (u)} d u}

L = \lim_{A \to \infty} {- \frac{\ln (A)}{A} \int_{x = 1}^{x = A} \frac{1}{\ln^{2} (u)} d u}

l i m i t o f \frac{\ln (A)}{A} = \frac{1}{A} a s A \to \infty = 0

0 \times c o n s t a n t = 0

c o n t i n u e

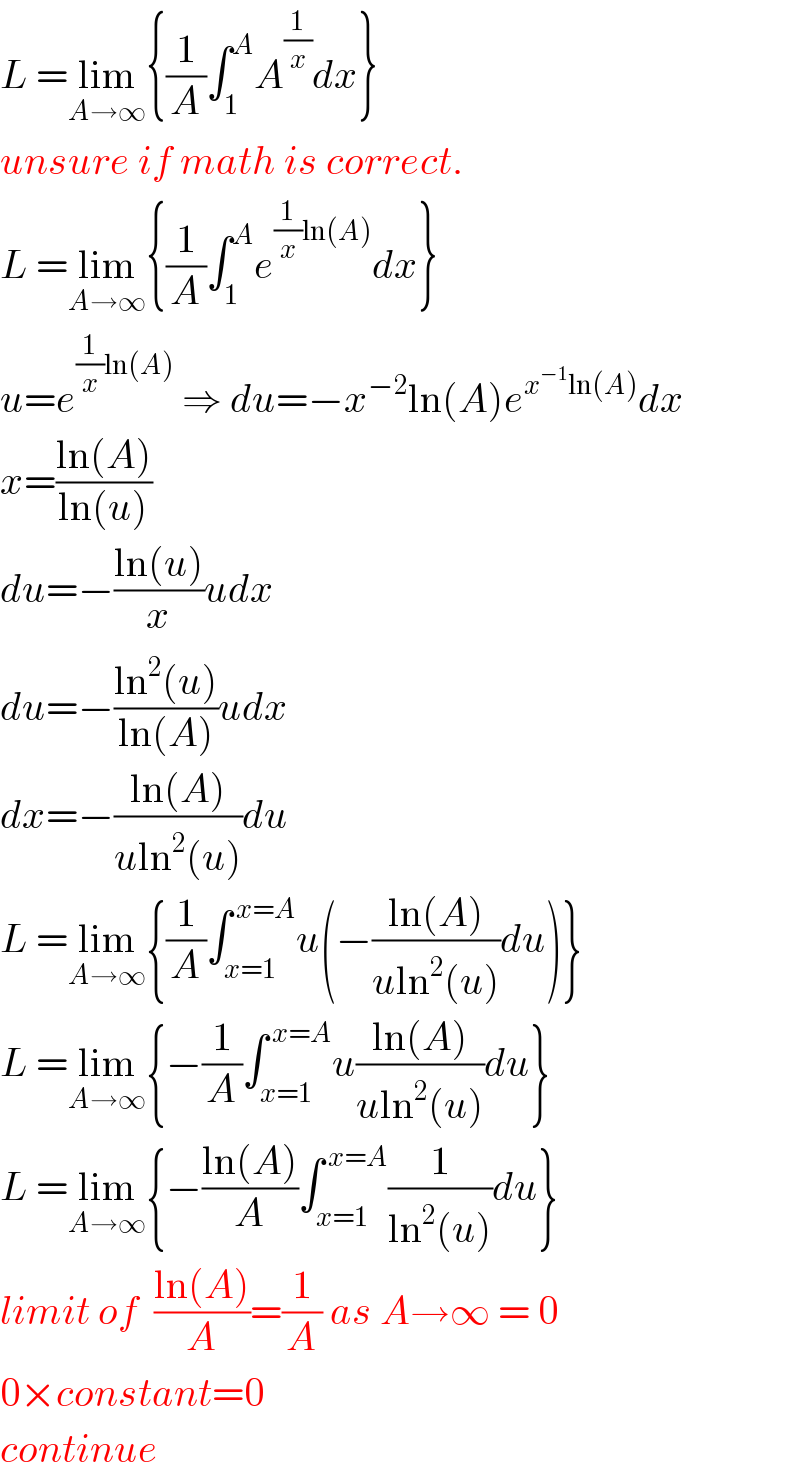
Commented by FilupSmith last updated on 01/Sep/16

\int \frac{1}{\ln^{2} (u)} d u

t = \ln^{2} (u)

u = e^{t^{1 / 2}}

d t = 2 \ln (u) \frac{1}{u} d u

\frac{u}{2 \ln (u)} d t = d u

\frac{e^{t^{1 / 2}}}{2 t^{1 / 2}} d t = d u

L = \lim_{A \to \infty} {- \frac{\ln (A)}{A} \int_{x = 1}^{x = A} \frac{1}{\ln^{2} (u)} d u}

L = \lim_{A \to \infty} {- \frac{\ln (A)}{A} \int_{x = 1}^{x = A} \frac{e^{t^{1 / 2}}}{2 t^{3 / 2}} d t}

c o r r e c t ? ? ?

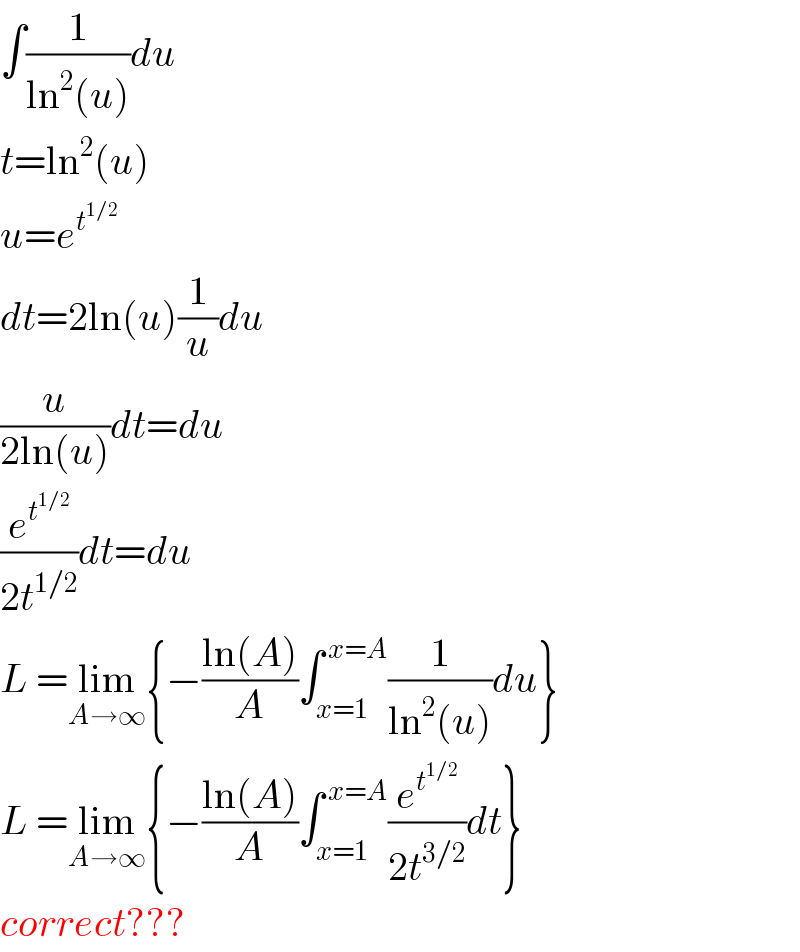
Commented by Yozzia last updated on 01/Sep/16

S o f a r i t s e e m s o k . I c a n a c c e s s t h e

s o l u t i o n o n l i n e, b u t I {d o n}^{'} t k n o w i t .

{I t}^{'} s a q u e s t i o n f r o m t h e 2015 I n t e r n a t i o n a l

M a t h e m a t i c s C o m p e t i t i o n f o r U n i v e r s i t i e s .

J u s t r e c e n t l y I g o t w i n d o f t h i s c o m p e t i t i o n

a n d n o w I h a v e a c c e s s t o a v a r i e t y o f

i n t r i g u i n g p r o b l e m s w h i c h I^{'} l l h o p e f u l l y

b e a b l e t o s o l v e a s I p r o g r e s s i n m y

u n d e r g r a d u a t e s t u d i e s . I^{'} m h o p i n g

t o s h a r e s o m e o f t h o s e p r o b l e m s h e r e

w i t h t h e f o r u m!

Commented by FilupSmith last updated on 02/Sep/16

That is awsome . I have no formal education .

I am completely self taught and you have

taught me lot!

Commented by Alimurtaza last updated on 05/Jan/17