Menu Close

Consider-a-triangle-ABC-Let-D-and-E-are-two-points-on-AB-and-AC-respectively-such-that-DE-BC-Now-there-are-two-parts-of-ABC-ADE-and-trapizoid-DBCE-If-these-two-regions-have-same-area-W

Tinku Tara 0 Comments
Pin




Question Number 3823 by Rasheed Soomro last updated on 21/Dec/15
Consider a triangle ABC. Let D and E are two points on AB and AC respectively such that DE ∥ BC. Now there are two parts of △ABC : △ADE and trapizoid DBCE. If these two regions have same area What will be the ratio of two distances : (i) distance of DE from point A and (ii) distance between BC and DE ?
$${Consider}\:{a}\:{triangle}\:\mathrm{ABC}.\:{Let}\:\mathrm{D}\:\:{and}\:\:\mathrm{E} \\ $$$${are}\:{two}\:{points}\:{on}\:\mathrm{AB}\:\:{and}\:\:\mathrm{AC}\:{respectively} \\ $$$${such}\:{that}\:\mathrm{DE}\:\parallel\:\mathrm{BC}.\:{Now}\:{there}\:{are}\:{two} \\ $$$${parts}\:{of}\:\bigtriangleup\mathrm{ABC}\::\:\bigtriangleup\mathrm{ADE}\:\:\:{and}\:\:{trapizoid} \\ $$$$\mathrm{DBCE}.\:{If}\:{these}\:{two}\:{regions}\:{have}\:{same}\:{area} \\ $$$${What}\:{will}\:{be}\:{the}\:{ratio}\:{of}\:{two}\:{distances}\:: \\ $$$$\left({i}\right)\:{distance}\:{of}\:\mathrm{DE}\:{from}\:{point}\:\mathrm{A}\:{and} \\ $$$$\left({ii}\right)\:{distance}\:{between}\:\mathrm{BC}\:{and}\:\mathrm{DE}\:\:? \\ $$
Commented by prakash jain last updated on 21/Dec/15
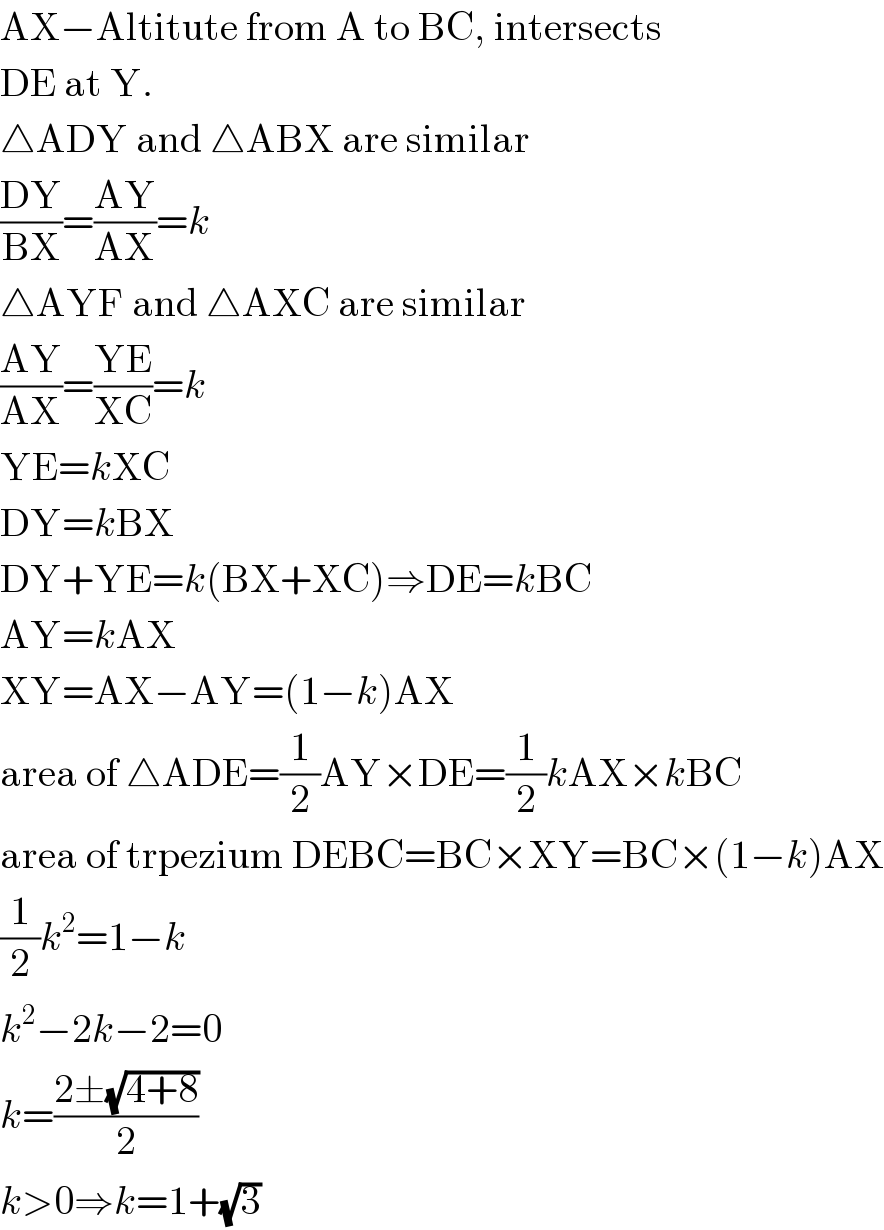
AX−Altitute from A to BC, intersects DE at Y. △ADY and △ABX are similar ((DY)/(BX))=((AY)/(AX))=k △AYF and △AXC are similar ((AY)/(AX))=((YE)/(XC))=k YE=kXC DY=kBX DY+YE=k(BX+XC)⇒DE=kBC AY=kAX XY=AX−AY=(1−k)AX area of △ADE=(1/2)AY×DE=(1/2)kAX×kBC area of trpezium DEBC=BC×XY=BC×(1−k)AX (1/2)k^2 =1−k k^2 −2k−2=0 k=((2±(√(4+8)))/2) k>0⇒k=1+(√3)
$$\mathrm{AX}−\mathrm{Altitute}\:\mathrm{from}\:\mathrm{A}\:\mathrm{to}\:\mathrm{BC},\:\mathrm{intersects} \\ $$$$\mathrm{DE}\:\mathrm{at}\:\mathrm{Y}. \\ $$$$\bigtriangleup\mathrm{ADY}\:\mathrm{and}\:\bigtriangleup\mathrm{ABX}\:\mathrm{are}\:\mathrm{similar} \\ $$$$\frac{\mathrm{DY}}{\mathrm{BX}}=\frac{\mathrm{AY}}{\mathrm{AX}}={k} \\ $$$$\bigtriangleup\mathrm{AYF}\:\mathrm{and}\:\bigtriangleup\mathrm{AXC}\:\mathrm{are}\:\mathrm{similar} \\ $$$$\frac{\mathrm{AY}}{\mathrm{AX}}=\frac{\mathrm{YE}}{\mathrm{XC}}={k} \\ $$$$\mathrm{YE}={k}\mathrm{XC} \\ $$$$\mathrm{DY}={k}\mathrm{BX} \\ $$$$\mathrm{DY}+\mathrm{YE}={k}\left(\mathrm{BX}+\mathrm{XC}\right)\Rightarrow\mathrm{DE}={k}\mathrm{BC} \\ $$$$\mathrm{AY}={k}\mathrm{AX} \\ $$$$\mathrm{XY}=\mathrm{AX}−\mathrm{AY}=\left(\mathrm{1}−{k}\right)\mathrm{AX} \\ $$$$\mathrm{area}\:\mathrm{of}\:\bigtriangleup\mathrm{ADE}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{AY}×\mathrm{DE}=\frac{\mathrm{1}}{\mathrm{2}}{k}\mathrm{AX}×{k}\mathrm{BC} \\ $$$$\mathrm{area}\:\mathrm{of}\:\mathrm{trpezium}\:\mathrm{DEBC}=\mathrm{BC}×\mathrm{XY}=\mathrm{BC}×\left(\mathrm{1}−{k}\right)\mathrm{AX} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{k}^{\mathrm{2}} =\mathrm{1}−{k} \\ $$$${k}^{\mathrm{2}} −\mathrm{2}{k}−\mathrm{2}=\mathrm{0} \\ $$$${k}=\frac{\mathrm{2}\pm\sqrt{\mathrm{4}+\mathrm{8}}}{\mathrm{2}} \\ $$$${k}>\mathrm{0}\Rightarrow{k}=\mathrm{1}+\sqrt{\mathrm{3}} \\ $$
Commented by Rasheed Soomro last updated on 21/Dec/15
A Novel Method!
$$\mathcal{A}\:\mathcal{N}{ovel}\:\mathcal{M}{ethod}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *