Question Number 1395 by Rasheed Soomro last updated on 28/Jul/15

Commented by prakash jain last updated on 28/Jul/15
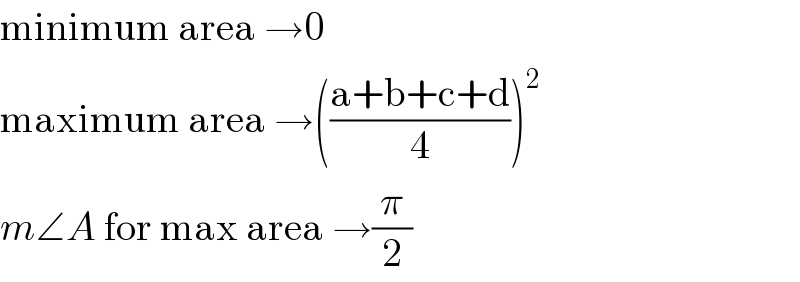
Commented by Rasheed Soomro last updated on 29/Jul/15

Commented by Rasheed Soomro last updated on 29/Jul/15
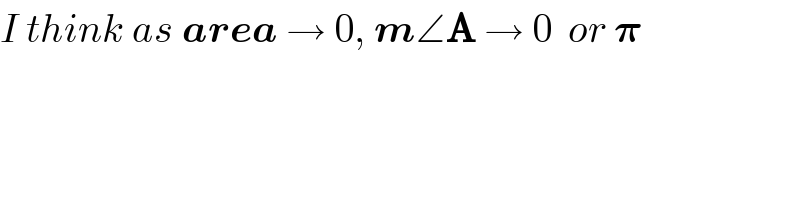
Commented by prakash jain last updated on 29/Jul/15
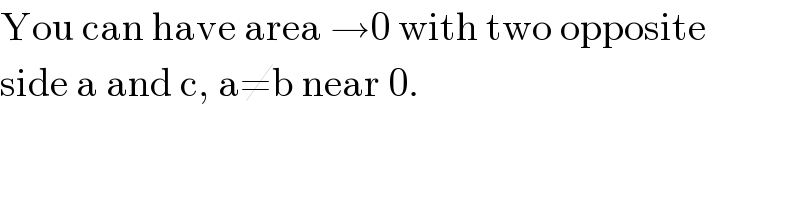
Commented by Rasheed Ahmad last updated on 31/Jul/15

