Question Number 138219 by otchereabdullai@gmail.com last updated on 11/Apr/21

Answered by bobhans last updated on 11/Apr/21
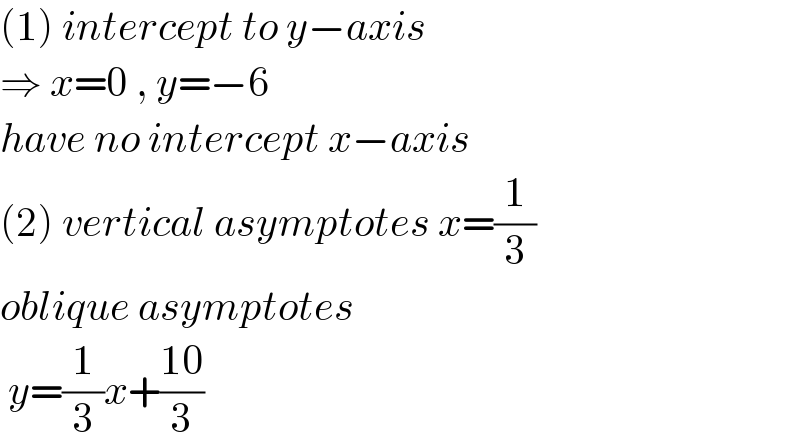
Commented by bobhans last updated on 11/Apr/21
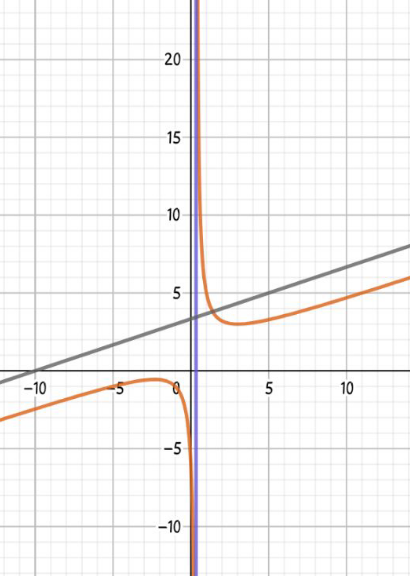
Commented by otchereabdullai@gmail.com last updated on 11/Apr/21

Answered by EDWIN88 last updated on 11/Apr/21

